

出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,
p.10-101
図表 分布のチェック項目
1 データ分析、解釈のプロセス
2 予備分析
3.Rによる予備分析
1 データ分析、解釈のプロセス
1) アンケートを実施した場合を例として、データを処理するプロセスをまとめた。
質問紙の作成、サンプリング、実査
↓
無効サンプルのチェック
↓
コーディング データをどのように入力するかを、後の分析計画を考えながら決定する。
↓
入力フォームの作成
↓
データ入力 誤りのないようにデータを入力。
↓
データ読み込み パソコンの統計パッケージなどで読み込む。
↓
データの前処理 無効データの再チェック、入力データにミスがないか、無効サンプルはないかを再チェック
欠損値の処理も行っておく。
↓
予備分析 本分析に入る前に、単純集計表などを作成して、回答者全体の特性を把握する。また、
本分析で使う手法で仮定されている条件を満たしているかをチェックする。
↓
本分析・解釈 仮説を検証するために分析を行う。必要ならば多変量解析なども行う。分析の結果を解釈する。
↓
結論・提言の報告 分析を踏まえて結論や提言をまとめ、報告する。
2)データ処理のプロセスでの留意事項
(1)サンプル、データの無効チェック
・欠損値:回答すべき質問に回答していない場合は欠損値となる。
・無効なサンプル:無回答が多い。回答はされているが、いい加減なサンプルは無効とする。
回収されたサンプルのうち、無効なサンプルを除いたサンプルを分析に使う「有効サンプル」とする。
どのようなサンプルを無効と扱うかは、いろいろ。
欠損値が一つでもある場合に無効とする。→ サンプル数が十分な場合にはこうしても差し支えはないことが多い。
欠損値が少しでもある
欠損値があっても、サンプル全体の平均値で置換してしまう。
注意:「系統的」に欠損値がある場合
特定の属性をもつ回答者が回答していない。
特定の質問に無回答が多い。
→調査票の設計に問題がある可能性がある(答えにくい質問、わかりにくい質問)。
その質問によって基準変数を測定しようとしていたような場合、致命的な欠陥になる可能性もある。
そのようなことを避けるために、調査する場合は、質問紙のプリテストを十分にすることが必要。
(2)コーディング coding
回答されたデータをどのように入力するかを決めるのがコーディング。文字や記号でもよいが、後の処理を考えると数字の方が楽。測定尺度によっていろいろな方法がある。
|
|
|
||
| 順序尺度、間隔尺度、比率尺度 | 間隔尺度、比率尺度などで測定されたメトリックデータについては、そのまま数字として入力すればよい。 | ||
| 名目尺度 | マルチプルアンサー | 選択肢の数だけの変数を用意し、選択された場合1、されなかった場合には0となるようにコード化する。
「無回答」という選択肢をつくり、無回答の場合には、それを1にする。 例 Q「缶コーヒー」は、どこで買うことが多いですか。次の中から多い順に3つまで○をつけてください(○は3つまで)。
→7つの選択肢に対応する変数 x1〜x7を定義。
選択肢1,4,5に○がついた場合には、
無回答の場合
|
|
| シングルアンサー | ・一つの変数に分類番号を入力する場合
○がついた選択肢の番号をそのまま入力する。 例 あなたが普段もっともよく使う交通機関は何ですか?(○は1つだけ)
|
||
| ・ダミー変数を定義する場合
シングルアンサーの質問で設定された選択肢の数が n個ある場合、0もしくは1の値をとる n-1個の変数(ダミー変数 dummy variable)を定義。 例 あなたは買い物にいくとき、どのような交通機関をつかいますか?使うものをすべてお選び下さい。(○はいくつでも)
x1=1 :「1.車で」に○がついたときに1、その他は0
実際には、一つの変数で入力した後、計算プログラムでダミー変数を生成することの方が多い。 |
|||
(3)入力フォームの用意
エディタでも入力できるが、ExcelやLotus1-2-3といった表計算ソフトで入力すると楽。
入力に使うフォームを用意しておく(ホームページのensdat1.exlを参照)。
・変数名の定義
変数名も決定して入力しておくと良い。
後での分析で、わかりやすい変数名にする。→SASでは8文字以内(大文字、小文字の区別なし)。
内容を表すような名前を付ける。
体系的な変数名にする。
同じ質問の中の選択肢は、同じアルファベットではじめる。 など。
図表 変数名の例
|
|
|
|
|
| Q1.あなたは買い物にいくとき、どのような交通機関をつかいますか?使うものをすべてお選び下さい。(○はいくつでも)
1.車 2.歩き 3.電車 4.自転車 Q2.あなたはテレビでどのような番組をごらんになりますか?ごらんになるものをすべてお選び下さい。(○はいくつでも)
|
CAR
DRAMA
わかりやすいがどの質問の選択肢なのか、区別されていない。 |
Q11
Q21
どの質問の選択肢なのか、区別されているが、中味が何なのか、わかりにくい。 |
TCAR
WDRAMA
体系的で、選択肢の中味もわかりやすい。 |
(4)データ入力
コーディング計画に基づいて、データを入力。
くれぐれも誤りのないように。
(5)データ読み込み
入力された変数を統計パッケージなどで読み込む。
パッケージで読み込むためには、パッケージの使い方を理解し、変数名を定義し、プログラムしなければならない(パソコン版の統合パッケージでは、テキストデータを読み込み、スプレッドシート形式で変数名を入力すればよいものもある)。
(5)データの前処理
無効データの再チェック、欠損値等の補正などを行う。
(6)予備分析
本分析に入る前に、単純集計表などを作成して、回答者全体の特性を把握する。また、本分析で使う手法で仮定されている条件(正規性)を満たしているかをチェックする(次節でくわしく)。
(7)本分析・解釈
検証したい仮説がある場合、それに適した分析を行い、仮説を検証する。必要ならば多変量解析を行う。
(8)結論・提言の報告
2 予備分析
データの準備、読み込みについてはII章を参照。
(1)予備分析の目的
予備分析とはなにかという厳密な定義はない。ここでは、最終的な分析の前に行う分析のことを予備分析と考えている。
・データのチェック
入力ミスなどはないか?
・データの全体像の把握
平均値は?男性の割合は? など利用するデータの全体像
・分析の前提の確認
正規分布しているか?
異質なサンプルが混在していないか?
→仮説を発見する可能性もある。
(2)いろいろな予備分析の方法1
変数の尺度 ノンメトリックかメトリックか?
変数の数 1つか2つか?
1変数(1次元データの分析)→一つの変数の分布をみる。
2変数(1次元データの分析)→二つの変数の関係をみる。
方法 図表を用いるか?代表値を用いるか?
代表値:分布を代表する・記述2
する値
度数分布やヒストグラムは視覚的情報に頼っているが、代表値は数量的概念に依っている。
多変量解析の各手法では、これらの代表値を用いて演算が行われる。
図表 予備分析の方法
| 変数の数 | 図表による記述 | 代表値による記述 | |
| メトリックな変数 | 1変数(1次元データの分析) | ヒストグラム hist()
箱ヒゲ図 boxplot() 幹葉図 stem() |
平均値 mean()
分散 var() 標準偏差 sqrt(var()) など |
| 2変数(2次元データの分析) | 散布図 plot() | 相関係数 cor()
共分散 var() |
|
| ノンメトリックな変数 | 1変数 | 単純集計表 table()
ヒストグラム hist() |
度数、割合、適合度・一様性についてのχ2値 |
| 2変数 | クロス集計表 table() | 独立性についてのχ2値
(同上) |
注)カッコ内はその分析を行うための代表的なRの関数名。
・変動係数
データの散らばり具合が同じと考えられる場合には、平均値をそのまま比較できる。
しかし、次のような場合にはどうするか?(架空の値)
1980年の47都道府県の所得の標準偏差は102万円だったが、1995年には130万円になった。15年間に所得の格差が拡大したといえるのか?
→この間に平均所得も400万円から450万円に上昇した。
変動係数=標準偏差/平均 を比較すると 80年:0.255 95年:0.288となり、所得の格差が拡大したことがわかる。
・分布の形状と歪度、尖度


出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,
p.10-101
図表 分布のチェック項目
|
|
|
|
| 位置 | データがどのような値を中心に散らばっているか? | 平均、メディアン、最頻値(モード) |
| 散布度 | データがどの程度散らばっているか? | 標準偏差、分散、4分偏差、レンジ(範囲=最大値-最小値) |
| 歪み | データの分布が左右対称か? | 歪度 skewness
左右対称な場合には0。右に裾を引いていれば正、逆ならば負。 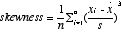 |
| 尖り | データの分布が裾をどのように引いているか? | 尖度 kurtosis
一様分布のように裾が切れた分布では負。どちらの側でも、長い裾を引く場合には正。 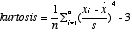
正規分布の場合 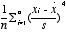 =3となる。 =3となる。 |
| 多峰性・単峰性 | データの分布に峰がいくつ見られるか? | ?図示しないとわからない。 |
| はずれ値 | 他のデータから極端に離れたデータはないか? | ?図示しないとわからない。 |
・二つの変数の図表による分析:散布図
二つの変数を縦軸と横軸にとってプロットしたもの。

出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,p.44
・二つの変数の代表値による分析:共分散、相関係数
変数xjと変数xkとの標本共分散
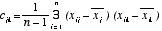

出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,p.50
・変数xjと変数xkとの相関係数(-1〜1までの値をとる)
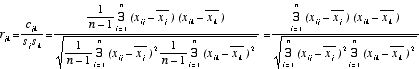
注)3にみえるのは Σ の誤り。
 |
  |
出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,p.18-19
右にゆがんだ(裾を引いた)分布 双峰型のヒストグラムの例


出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,p20
同じデータについて持家、借家別にプロットすると二つのピークは、それぞれのピークに対応していることがわかる。


出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,p.20-21
・2次元データの分析
分割表(クロス集計表)

出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,p.45
・メトリックな変数をカテゴリー化することによってクロス集計表を作成することもできる。

出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会,p.47
○図表による分析の重要性


出所)二木宏二、朝野煕彦(1991),『マーケティング・リサーチの計画と実際』,日刊工業新聞社,p.158
相関係数は同じでも、グラフを描いてみると、それぞれ異なった関係があることがわかる。
左下の場合は1つだけ、他と異なった傾向を示す異常値、はずれ値outlierであることがわかる。はずれ値となっている理由を検討する。(入力ミス、測定ミスなどはないか?)

出所)東京大学教養学部統計学教室編(1992),『統計学入門』,東京大学出版会
プロットすることによって白色矮星と赤色巨星のグループが見いだされた。

出所)片平秀貴(1987),『マーケティング・サイエンス』,東京大学出版会,p.257
グラフ→非常に多くの情報を与えてくれる。
代表値に頼ることは危険。グラフでパターンを把握しておくことが必要。いきなり高度な分析をする前に、予備的な分析、特にグラフ化しておくことが重要。
-
3.Rによる予備分析
|
#演習用データ読み込み #データフレームに読み込み ossdata<-read.delim("osssub.dat") #ファイル名は""でくくる。Rと同じディレクトリの場合にはディレクトリの指定は不要。
#読み込めたか確認のために一番左の変数と一番右の変数を出力してみる
#全データを出力
#含まれる変数idのみを出力
#ossdataに各種の変数が格納されている。そのうちnofdlに注目。 ##1変数の代表値 #平均
#分散
#標準偏差
summary(ossdata$nofdl) ##1変数の図表 #ヒストグラムを書く
#幹葉図 ヒストグラムよりも情報が多い
#ボックスプロット
#2変数
#共分散
#散布図
#集計表
|
2
統計学は次の3つの分野に大別される。
・記述統計学 集団としての特徴を記述するために、観測対象となった各個体について観測し、得られたデータを整理・要約する方法。
・統計的推測 サンプルから母集団の特徴を推定する。
・統計的決定 データに基づいて具体的な問題に決定を下す。