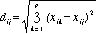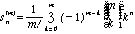DD-IV-5cluster

5 サンプルの分類：クラスタ分析

1)クラスタ分析の考え方
2)階層型クラスタ分析と非階層型クラスタ分析
3)クラスタ分析の手順
4)階層型クラスタ分析 hierarchical clustering
5)Rによる階層型クラスタ分析
6)非階層クラスタ分析 non-hierarchical clustering
7)Rによる非階層的クラスタ分析
8)クラスタ分析の問題点

1)クラスタ分析の考え方
・適用例
例1)動植物の種、目の分類

例2)マーケット・セグメンテーション¹
　　「市場を何らかの意味で同質な消費者グループに市場を分割し、そのいずれかにターゲットを絞ることによって、マーケティング活動をより有効に展開する(片平 1987,p.97)」

・クラスタ分析の考え方
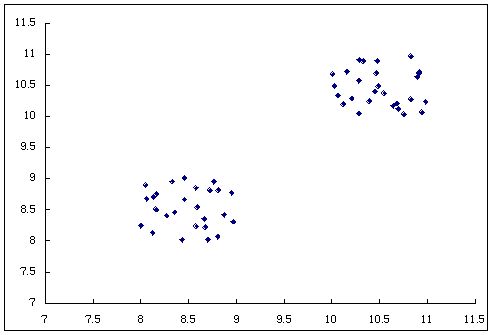
　二つの変数をプロット。
　二つの塊（クラスタ）が見られる。
　クラスタ分析→特性が類似しているサンプルを塊（クラスタ）にまとめる手法。

・サンプル間の距離
　どのようにしてクラスタをつくるか？
　サンプル間の距離もしくは類似度を用いる。
　　（距離が小さいサンプルをクラスタにまとめる、類似度が高いサンプルをクラスタにまとめる）
　距離、類似性の指標としては、（一般化された）ユークリッド距離が最もよく用いられる² 。

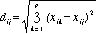
　x_ik確率変数 X_kのサンプル iについての観測値、x_ij確率変数 X_kのサンプル jについての観測値　　　　変数はp個。

→変数の単位が異なる場合には、変数を標準化して分析する。
　変数間には相関がない方がよい。→変数の数が多い場合には、因子分析、主成分分析によって変数を集約した因子を抽出して、これを用いてクラスタ分析を行う。

・クラスタ間の距離
　クラスタが複数できた場合、「クラスタ間の距離」が短い（類似度が高い）ものをさらにクラスタにまとめていく（1サンプル=1つのクラスタと考えてもよい）。
　クラスタ間の距離の考え方にはいろいろある。

図表　いろいろなクラスタ間の距離の定義方法

	概要	特徴
最短距離法 nearest neighbor method	2つのクラスタ間の距離を、各クラスタの任意の2サンプル間の距離で定義し、距離がもっとも近いクラスタを併合する。	もっとも近いサンプルを含むクラスタを併合するので、鎖(chain)状のクラスタができやすい。
最長距離法 farest neighbor method	2つのクラスタ間の距離を、各クラスタの任意の2サンプル間の距離で定義し、距離がもっとも近いクラスタを併合する。	併合されなかった部分は併合された部分から離れる傾向がある。
重心法 centroid method	2つのクラスタ間の距離を、各クラスタの重心の距離で定義し、距離がもっとも近いクラスタを併合する。	最短距離法、最長距離法では、クラスタに含まれている一つのサンプルの情報しか利用していないが、重心法ではすべてのサンプルの情報を利用していることになる。
群平均法 group average method	2つのクラスタ間の距離を、各クラスタに含まれる全サンプル間の平均距離で定義し、距離がもっとも近いクラスタを併合する。	重心法と比べて、空間の濃縮や拡散が行われにくい。
ウォード法 Ward method	同じクラスタには、類似するサンプルが含まれるべきであり、併合後のクラスタ内での分散の増加分がもっとも小さくなるような二つのクラスタを併合していく。　l 番目のクラスタと m 番目のクラスタそれぞれの平方和をS_l,S_mとする。　これらを併合したあとのクラスタ lm の平方和をS_lmとすると、　S_lm=S_l+S_m+△S_lm　ここで、△S_lm=S_lm-S_l-S_mは、二つの異なるクラスタを併合したことによって増加した平方和。　△S_lmをすべてのクラスタの組み合わせについて計算して、もっとも小さいクラスタを併合する。	同じクラスタ内のサンプルはできるだけ一様で、異なるクラスタ間のサンプルはできるだけ異なっているように併合されることになる。　実用上、よい結果を示すので使われることが多い。

出所）浅野長一郎、江島伸興(1996),『基本多変量解析』,日本規格協会,ch.10および、朝野煕彦(1996),『入門　多変量解析の実際』,講談社サイエンティフィック,ch5での記述を参考にして作成。

2)階層型クラスタ分析と非階層型クラスタ分析
　

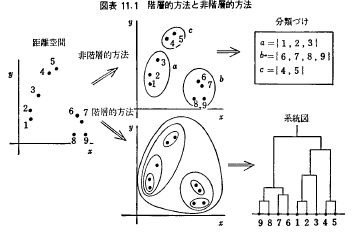
出所）本多正久、島田一明(1977)『経営のための多変量解析法』産業能率短期大学出版部,p.156

　どちらを用いるかは目的にもよるが、それぞれの利点、問題は次の通り。

図表　階層クラスタ分析と非階層クラスタ分析の比較

	階層クラスタ分析	非階層クラスタ分析
利点	・解釈が容易・クラスタ数をあらかじめ決めなくても良い。	・信頼性が高い。　クラスタ間での移動を認めているので、初期の段階での誤りを回復できる。・処理が速い。
問題点	・相対的に不安定で信頼性に乏しい　ツリー状に分割を進めていくので、初期の段階で分割が誤っていた場合には、その後の分析にの意味がなくなる。　初期のわずかな違いによって、大きな違いが生じてしまう。・サンプルの数が多いと、樹形図が巨大になり、解釈しにくい。・クラスタ数を事後的に決定することについての批判もある。	・解釈が困難な場合がある。・クラスタ数を決定する客観的基準が未確立。

出所）Aaker, David A.,V. Kumar, and Gorge S. Day,(1995),Marketing Research 5th ed.,Prentice Hall: NJ, p.330
および朝野煕彦(1996),『入門　多変量解析の実際』,講談社サイエンティフィック,p.77より作成。

3)クラスタ分析の手順

　階層型で数の目安をつけてから非階層型で最終決定する手順を想定。

　例)マーケットセグメントの場合

　クラスタ分析する変数の選択
　　↓
　（必要ならば）変数を平均0、分散1に正規化
　　↓
　（必要ならば）変数を因子分析、主成分分析などによって変数を集約
　　　　　　　　似たような変数が沢山あると、それらが距離の計算に大きな貢献をしてしまう。
　　↓
　予備分析　　クラスタする変数を縦軸、横軸にして、各サンプルをプロット
　　　　　　　クラスタがみられるか、はずれ値はないか、などを確認しておく。
　　↓
　階層的クラスタ分析の実施→分割するクラスタ数の検討（ただし、サンプル数が多いと実行できない）
　　↓
　(必要ならば)非階層的クラスタ分析→いくつかの分割数を指定して実施。
　　↓
　　(必要ならば)クラスタの特徴の分析→どのような変数に違いがみられるか、クラスタの大きさは？などをチェック。
　　　　　　　　　　　　　あまり小さなクラスタをつくっても、それ以降の分析ができなくなる。
　　　　　　　　　　　　　　例　クラスタ別に回帰分析しようと思っても、そこに含まれるサンプル数が不足する。
　　　　　　　　　　　　　　　　マーケティング的に、小さなクラスタには意味がない。など）。
　　↓
　クラスタ分割の安定性の検討　分析するサンプルを変えたりしても同じ結果になるか?
　　　　　　　　　　　　　　　クラスタ分割を前提として、判別分析を行うなど。
　　↓
　クラスタ数の最終決定。
　　クラスタ間での違いが明確にわかり、かつ各クラスタの大きさも適切なものを最終的に選定する。

4)階層型クラスタ分析 hierarchical clustering

・手順
　類似度が高いもの（距離が小さいもの）を同じクラスタにまとめていく。
　あるサンプルを、それともっとも近いサンプルが含まれているクラスタに含めていく（最短距離法）。
　最終的に1つのクラスタになるまで併合を続ける。この過程をまとめると、樹形図dendrogramが得られる。

図表 5つのサンプル間の距離

	A	B	C	D
A
B	2
C	4	4
D	4	4	3
E	5	5	5	5

図表上のサンプルについての樹形図

6
5 ------------
4 --------- |
3 | ---- |
2 ---- | | |
1 | | | | |
　A B C D E

5)Rによる階層型クラスタ分析

dist(データセット,method = "euclidean") 　　データセットについて距離の計算を行う。

指定しなければユークリッド距離が使われる。
　0/1データとのきはbinaryの方が適切。
　その他の距離の定義については
?dist
で参照。

hclust(距離データセット,method = クラスタ間の距離の計算方法,labels=ツリーを書くときのラベルとなる変数)　　距離データ(非類似度)セットを用いて階層型のクラスタ分析を行う。

入力は生の変数ではなく、距離データセット。
相関行列など類似度データの場合でも、マイナスをつけるなどすれば非類似度データとできるので適用可能。
サンプル数が多いと計算量が多くなって、エラーになる場合もある。そのような場合は、非階層型のクラスタ分析をする。
library(mva)
使う前にとしておく必要がある。
　クラスタを併合するための距離の計算にはデフォルトではcompleteだがマーケティングでの適用の場合、"ward"の方が安定するとのこと。
labels=にサンプル番号などを指定しておくと樹形図が読みやすくなる。

plclust(階層型クラスタ分析の結果データ,labels = )　階層型クラスタ分析の結果を樹形図として出力

labels=にサンプル番号などを指定しておくと樹形図が読みやすくなる。

図表　クラスタ分析のための予備的分析、前処理

#10個の変数について
a<-data.frame(ossdata$nrelease,ossdata$npcntb,ossdata$ncntb,ossdata$nmsgfr,ossdata$npml,ossdata$nmsgml,ossdata$npfrq,ossdata$nmsgfrq,ossdata$npbug,ossdata$nmsgbug)

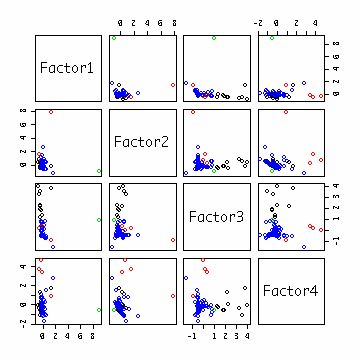
#変数を組み合わせて目で見てみる。かたまりがあるか?
pairs(a)

#変数の数が多いので前回行った通り、因子分析によって4つの因子を抽出。それを用いてクラスタ分析する。
library(mva)
f<-factanal(a,factors=4,rotation="varimax",scores="regression")
pairs(f$scores)

#ユークリッド距離を計算する
#ただし、変数間で単位がちがうので正規化しておく方が適切
ds<-dist(f$scores,method="euclidean")
ds
#これがサンプル間の距離
# 1 2 3 4 5 6 7
#2 2.2221179
#3 0.9583827 1.845037
#4 0.4944091 2.127946 0.53677830
#5 0.8129004 2.018656 0.21703078 0.3552084

summary(ds)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 0.01085 0.39980 0.95450 1.71200 2.03600 12.95000

#これについて階層型クラスタ分析。クラスタ間の距離はWard法で。
cl<-hclust(ds,method="ward")
names(cl)
#[1] "merge" "height" "order" "labels" "method"
#[6] "call" "dist.method"

cl$merge
#クラスタ、サンプル併合の順番を示す(サンプル数-1行×2列)
#マイナスがついているのはサンプル番号。
#ついていなければ(j行目=j番目に形成された)クラスター番号。
#最初にサンプル31と39を併合した
# [2,] -36 -50
#[3,] -22 -69
# [4,] -89 2
#89番目のサンプルと2段階目で作成されたクラスタを併合
# [5,] -82 -92
# [6,] -77 -81
# [7,] -27 -66

#[94,] 90 93
#最後に90番目と93番目に形成されたクラスタを併合。

cl$height
#樹形図を描くときの高さ(サンプルやクラスターの距離)
#cl$mergeと同じく　サンプル数-1行ある。
#最初に距離0.01085のサンプルを併合した。min(ds)と一致している。
#
# [1] 0.01084570 0.01149270 0.01618843 0.01943137 0.01989555 0.02107168
# [7] 0.02381250 0.02649606 0.02798822 0.03615874 0.03663123 0.04384399
#[13] 0.04463339 0.05385823 0.05595344 0.06084169 0.07273703 0.07745055
#[19] 0.07901272 0.08449828 0.08928498 0.09324200 0.09496602 0.10227156
#[25] 0.10285960 0.11338776 0.11390144 0.11584701 0.11796974 0.13973116

#[79] 1.99061840 2.03058613 2.17353128 2.71122317 2.93270797 3.42022039
#[85] 3.62797497 4.28208498 4.58581697 6.84719490 7.04797309 11.57017711
#[91] 12.94732825 16.12306786 17.07955951 31.56859641

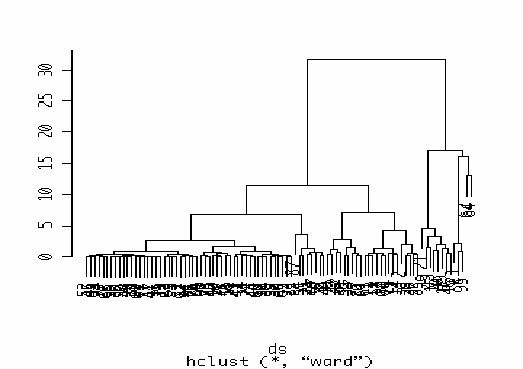
#クラスタ分析の結果を樹形図として出力
plclust(cl)
#距離15の場合、4クラスタ。10のとき6クラスタなど。

6)非階層クラスタ分析 non-hierarchical clustering
　n人をm個のクラスタに何らかの方法で分割。
　　>非階層クラスタ分析では、何個に分割するかを指定する必要がある。

　この組み合わせの数は次式で表される（第2種のスターリング数、ｸﾗｽﾀの大きさは任意）。

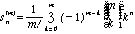
　例　25人を5つのクラスタに分類する組み合わせの数は2437兆通りになる。
→効率のよい分割方法が必要（サンプル数が大きい場合には、階層クラスタ分析を行うことができなくなる）。

→非階層クラスタ分析
　（クラスタ化の基準が改善されるならば、サンプルがあるクラスタを離れて、別のクラスタに属することができる）。

・分析のアルゴリズム³
(a)初期シードの選択
　分割するクラスタの数 kを与える。→これを与えないと分析できない。
　nサンプルからなんらかの方法で k個のサンプルを選ぶ。
　これらを大きさ1の初期クラスタ（初期シード）と考える。

(b)各サンプルのクラスタへの割当
　初期シードと残りのn-k個の各サンプルとの距離を計算して、距離が近いサンプルを各クラスターに併合する。
　併合した場合には、クラスターの重心を計算し、初期シードの値と置換する。
　以下同様の手順を繰り返して、サンプル数をすべてのクラスタに割り当てる。
　併合にともなってクラスタの重心の位置が変化するために、クラスタに属するサンプルも変化する可能性がある。このような変化が生じなくなるまで（もしくは重心の位置が大きく変化しなくなるまで）上記の手順を繰り返す。

7)Rによる非階層的クラスタ分析

kmeans(生の変数データセット,クラスタ数)　　非階層型のクラスタ分析を行う。

library(mva)
　を指定する必要あり。
クラスタ数を指定する必要がある。階層型クラスタの結果を参考にするのが一つの方法。

図表　非階層的クラスタ分析の例

#10個の変数について上と同様、因子分析する。
a<-data.frame(ossdata$nrelease,ossdata$npcntb,ossdata$ncntb,ossdata$nmsgfr,ossdata$npml,ossdata$nmsgml,ossdata$npfrq,ossdata$nmsgfrq,ossdata$npbug,ossdata$nmsgbug)

library(mva)
f<-factanal(a,factors=4,rotation="varimax",scores="regression")
#変数を組み合わせて目で見てみる。かたまりがあるか?
pairs(f$scores)
c2<-kmeans(f$scores,2)
c2

#$cluster
#サンプルが何番のクラスタに属するか
# [1] 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#[38] 1 1 1 1 1 2 1 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 2 1 1 1 1 1 1 1
#[75] 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2

#$centers
#各変数について、クラスタ毎に平均算出。それぞれのクラスタの特徴をみるとき有用。
# Factor1 Factor2 Factor3 Factor4
#1 -0.08727181 -0.1253379 -0.2809198 -0.1525953
#2 0.55048375 0.7905932 1.7719556 0.9625244

#クラスタ内での平方和
#$withinss
#[1] 71.31192 214.18528

#各クラスタに属するサンプル数
#$size
#[1] 82 13

#データの平方和を計算。var(x)=xの平方和/(サンプル数-1)
tss<-sum(diag(var(f$scores)))*(length(ossdata$id)-1)
wss<-sum(c2$withinss)
r2<-(tss-wss)/tss
r2

c3<-kmeans(f$scores,3)
c3
r3<-(tss-sum(c3$withinss))/tss
r3

c4<-kmeans(f$scores,4)
c4
r4<-(tss-sum(c4$withinss))/tss
r4

c5<-kmeans(f$scores,5)
c5
r5<-(tss-sum(c5$withinss))/tss
wss)/tss
r5

c6<-kmeans(f$scores,6)
c6
r6<-(tss-sum(c6$withinss))/tss
r6

c7<-kmeans(f$scores,7)
c7
r7<-(tss-sum(c7$withinss))/tss
r7

c8<-kmeans(f$scores,8)
c8
r8<-(tss-sum(c8$withinss))/tss
r8

c9<-kmeans(f$scores,9)
c9
r9<-(tss-sum(c9$withinss))/tss
r9

c10<-kmeans(f$scores,10)
c10
r10<-(tss-sum(c10$withinss))/tss
r10

#参考　クラスタ数を多くするとこの指標は1に近くなる
c95<-kmeans(f$scores,90)
r95<-(tss-sum(c95$withinss))/tss
r95

#クラスタ数検討のため計算したrsqを結合してプロット
rsq<-rbind(r2,r3,r4,r5,r6,r7,r8,r9,r10)
plot(rsq)

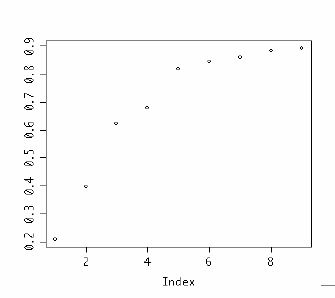
#プロットされている点は左からクラスタ数、2、3、4、5、、、
#3-4で急速にRsqは増加しているが、それ以降はクラスタ数を増加させても向上はなだらか。
#クラスタ数3-5についてサンプルサイズを見ると、4つにするとサンプル数1のクラスタが発生。
#
c3$size
c4$size
c5$size
#どのようにクラスタされるか、3と4　4と5との関係をみる
table(c3$cluster,c4$cluster)
# 1 2 3 4
# 1 0 0 1 0 3つでも4つでも、このクラスタは1つのサンプルによって構成されている。
# 2 8 4 0 0　　　3つのときは12サンプルだが4つにすると2つに分かれる
# 3 2 0 0 80

table(c4$cluster,c5$cluster)
# 1 2 3 4 5
# 1 0 0 0 0 10
# 2 3 0 1 0 0
# 3 0 0 0 1 0
# 4 1 79 0 0 0

#どのようにクラスタされたか見てみる
b<-data.frame(c2$cluster,c3$cluster,c4$cluster,c5$cluster,c6$cluster,c7$cluster,c8$cluster,c9$cluster,c10$cluster)
b

c2.cluster c3.cluster c4.cluster c5.cluster c6.cluster c7.cluster c8.cluster c9.cluster c10.cluster
1 1 3 4 2 5 4 1 9 3
2 1 3 4 2 6 2 3 5 2
3 1 3 4 2 5 4 1 9 6
4 1 3 4 2 5 4 1 9 6
5 1 3 4 2 5 4 1 9 6

60 1 3 4 2 5 4 1 9 3 このサンプルがひとつだけクラスタ。
61 1 3 4 2 5 4 1 9 3
62 2 1 3 4 2 5 4 8 10
63 1 3 4 2 5 4 1 9 6
64 1 2 2 3 4 6 6 6 9
データもみてみる
ossdata[60,]
id groupunixnam devstage nofdl oldestfiledate licgpl nlngengl oslinux osmicros ososind tpcsyste tpcsoftw
60 750 proxytools 5 261 2001-04-19 0 1 0 1 0 1 0
tpccommu tpcgames nrelease npcntb ncntb nmsgfr npml nmsgml nmsgmlmax npfrq nmsgfrq nmsgfrqmax npbug nmsgbug
60 1 0 9 3 673 0 1 2 2 1 1 1 0 0
nmsgbugmax
60 0

#4クラスタで決定。以下ではクラスタの特徴をみる。
#中心の座標　　どのような特徴があるか?
c4$centers

# Factor1 Factor2 Factor3 Factor4
#1 -0.27742055 0.01139631 2.5144529 0.002097627
#2 0.08725987 2.55256640 -0.1229022 3.164121341
#3 9.00307477 -0.92071899 0.9309722 -0.548848195
#4 -0.08222386 -0.11754387 -0.3197987 -0.151607668

#プロットしてみる。ただし、col=オプションでクラスタ番号に応じてプロットさせる色を変える。
pairs(f$scores, col=c4$cluster)

#必要ならば他の変数との関係(クラスタ別に集計など)をみて、各クラスタの特徴を把握。
table(c4$cluster,ossdata$oslinux)
table(c4$cluster,ossdata$tpcgames)

○クラスタ数決定の目安
・R-Squared　=クラスタ間分散/全分散
　　　　　　　　　　　　　　　　　　　　　　ただし、全分散=クラスタ間分散　+　クラスタ内分散
　クラスター分析→同じクラスター内では一様で（クラスタ内分散が小）、異なるクラスターでは大きく異なる（クラスタ間分散が大）であるように、サンプルを分割。
→クラスタ間分散/クラスタ内分散　が大きいほどよい。
　R-Squaredは0～1の値をとる。
　　0：　グループ間での差がない。
　　1：　グループ間での差が最大。

　横軸にクラスター数、縦軸にR-Squared、Semipartial R-Squaredをとってプロット。
　R-Squaredの値が急激に変化するところに注目して、クラスターの数の目安とする。

　ただし、R-Squared、Semipartial R-Squaredの値の分布は不明なので、統計的な検定はできない（例　クラスター数3とした場合と4とした場合のどちらがよいかを統計的には検定できない）。

8)クラスタ分析の問題点
　クラスタ分析の方法は次の要素を組み合わせた種類だけある。→いろいろな方法がある（ありすぎる）が、どれが最良な方法かは一概に決められない。
　　類似性の測度
　　クラスタ化の基準：どのサンプルを同じクラスタに属するとするか？
　　クラスタ法：階層的、非階層的
　　クラスタ数の決定
　　　事前に決める。
　　　何らかの基準によって決める。
　よって、同じデータでも異なるアルゴリズムでクラスタ分析を行えば、異なった結果が得られる可能性が高い。
→結果を評価するためには主観的な要素も必要となる。

・ほとんどのアルゴリズムでは、(d)(e)(f)のようなクラスタを検出することはできない。
　ここで紹介したような標準的なクラスタ分析手法では明確に分離することは困難。
→まずはプロットしてみる。

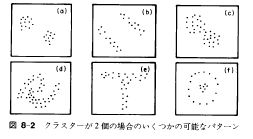
出所）Manly, Bryan F. J.(1971),Multivariate Statistical Methods: A Primer,(村上正康、田栗正章訳『多変量解析の基礎』,培風館,1992年,p.92)

・（ここで示したような標準的な）クラスタ分析は統計的検定の枠組みにのっていない。
　クラスタ数2がよいのか、3がよいのかといったことを統計的に検定できない。

¹ セグメントについては、以下の文献を参照。
片平秀貴(1987),『マーケティング・サイエンス』,東京大学出版会,ch4.マーケット・セグメンテーション
　　片平秀貴(1992),「マーケティングと競争」(大澤豊編『マーケティングと消費者行動　マーケティング・サイエンスの新展開』有斐閣),p.49-79

² この他の距離については、奥野忠一、久米均、芳賀敏郎、吉澤正(1971),『多変量解析法』,日科技連,p.395を参照。

³ ここでのアルゴリズムはほんの一例。初期シードの選択方法、シードへのサンプルの割当方法、クラスタの重心の計算のタイミングなど、いろいろなバリエーションがある。