5)回帰診断

　線型回帰分析は、下記の条件を前提としている。これらが成立しているかをチェックすることが必要。
　予備的分析をおこなっておけば、多くの問題は避けられる。

図表　線型の回帰分析での仮定

 

仮定

  症状/原因と対応策
関数形について ・線型性
　　被説明変数と説明変数には線形の関係がある。 		   
誤差項εについて ・誤差項の平均値は0
　E(εi)=0
・誤差項は(平均0、分散σ2の)正規分布に従う。
　εi〜N(0,σ2)




・誤差項の分散はσ2の一定値。
　Var(εi)=σ2
・誤差項は独立に分布。
　cov(εi,εi')=0
　
　βについてのt検定、モデル全体のF検定は、誤差項が正規分布することを前提としている。この仮定が満たされていない場合、検定結果も信頼できなくなる。 		・残差のヒストグラム
　正規分布しているか？
・Q-Qプロット
　残差が正規分布すると仮定したときの理論的な分布と現実の分布とを比較。

・はずれ値の検出
　Cookの距離

・予測値-残差プロット
　予測値と残差との間に系統的な関係がないか？
 		・はずれ値
　入力ミス
　変数変換
　分析から除外もしくは、はずれ値ダミー


・分散不均一
　変数変換
　　説明変数の追加
・系列相関
　時系列分析の場合、誤差が前期の誤差と相関していることもある。
・不適切な分布
　・二つの山がある場合は、グループ別に推定するか、ダミー変数を入れる。
　・変数変換する。

・説明変数の追加
説明変数間について ・説明変数はランダム変数ではなく、事前に選択もしくは固定されている。







・説明変数は誤差なく測定されている。





・説明変数は線型独立。
　推定結果が不安定になる。直感的にみておかしい符号がでる。
　例　地域別商業販売額を人口と世帯数で説明すると、例えば世帯の符号がマイナスになる。 		・実験ならばこの条件は満たされるが、そうでない場合は満たされていることの方が珍しい。このような場合には、因果性について結論づけることは極めて困難。
　例　人の子供の出生率を、こうのとり　の数で説明して有意であったとしても、こうのとり、が子供を運んでくるとはいえない。

・誤差の評価は困難。
　少なくとも、測定したい概念にふさわしい変数を選択すること。
　例　都市化や知能という概念にふさわしい変数は何か？


・説明変数間でのプロット
・説明変数間の相関係数の算出
・VIFの算出









・説明変数の誤差項を考慮した分析（共分散構造分析）などもあるが、この授業では割愛。




・相関が高い変数群がある場合、それらから、どれか一つのみを用いる。
・相関が高い変数群をなんらかの方法で集約する。
　例　適当な方法で指数を作成する。
　因子分析、主成分分析などを適用する。
観測について すべてのサンプルは同じように信頼できる。 ・評価は困難。  

出所）Chatterjee et al.(2000) Regression Analysis by Example, WileyのCh.4より作成。


(2)残差分析：誤差の正規性、はずれ値、線型性のチェック
　横軸に予測値やデータの時点、縦軸に残差をとりプロットすることによって診断情報を得ることができる。

　極端な値がある場合には、それを入れた場合と、入れない場合で推定結果が大きく異なってしまう。
→予備分析の段階で、ヒストグラム、グラフなどでチェックする。
　残差をチェックする。標準化残差が2以上の場合には、要注意。



出所）Hair, Jr., Joseph, Rolph E. Anderson, Ronald L. Tatham, and William C. Black,(1995),Multivariate Data Analysis with Readings 4th ed.,Prentice Hall: NJ, p.112



#先ほどのモデル2について残差プロットをみる。まずは回帰分析。

result2<-lm(nofdl~nrelease+tpcgames,ossdata)
summary(result2)

#Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 3058.4 2402.9 1.273 0.20631
#nrelease 481.2 149.0 3.229 0.00172 **
#tpcgames 14158.7 4995.9 2.834 0.00565 **
#---
#Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

#Residual standard error: 17230 on 92 degrees of freedom
#Multiple R-Squared: 0.175, Adjusted R-squared: 0.1571
#F-statistic: 9.758 on 2 and 92 DF, p-value: 0.0001435

#これでresult2の中に下記の変数が格納される。
names(result2)
# [1] "coefficients" "residuals" "effects" "rank"
# [5] "fitted.values" "assign" "qr" "df.residual"
# [9] "xlevels" "call" "terms" "model"

plot(result2)
#とすると自動で有用なプロットをしてくれる。
#推定された従属変数と残差とのプロット
#非線形性、はずれ値、分散不均一などのチェック
plot(result2$fitted,result2$residual)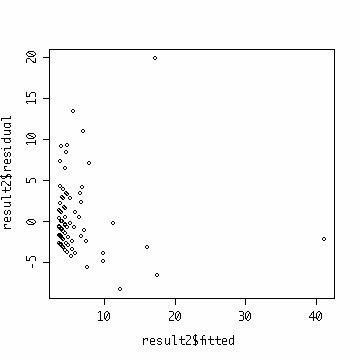



・残差と予測値
　非線形性がないか？
　予測値と残差に相関がないか？
　グループに分かれていないかなどを目で確認。
　数字はサンプルの番号

図表 　残差と予測値とのプロット




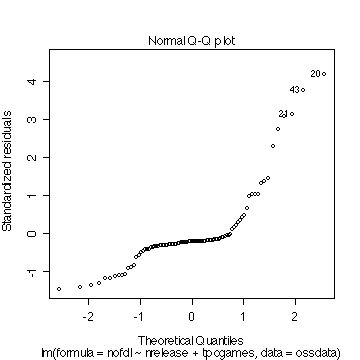
・４分位数プロット(Q-Qプロット)
　残差が正規分布する場合には直線上に並ぶ。

図表 　４分位数プロット(Q-Qプロット)



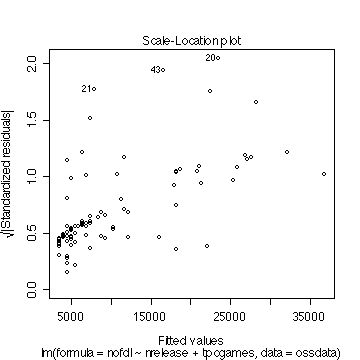
・標準化した残差と予測値とのプロット。
　一つ前のものと同じ読み方。ただし、残差が標準化されているので、標準化残差の絶対値が2よりも大きい場合、はずれ値outlierと考える、といった議論が可能。

図表 　標準化された残差と予測値とのプロット



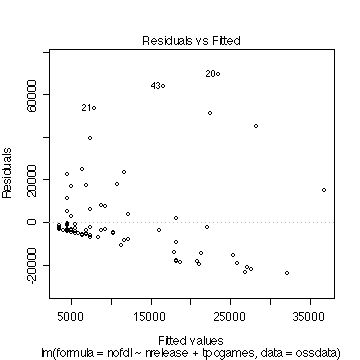
#20番目のサンプルのデータをみるには次のように指定すればよい。
ossdata[20,]
#同じく残差や予測値もみてみる
result2$residuals[20]
result2$fitted.values[20]

#同様に21、43も見てみる
ossdata[21,]
ossdata[43,]

#windows版の場合、edit(データセット名）　コマンドで直接、見ることが可能。
edit(ossdata)

#グラフにはサンプル番号が表示されるので、それを直接、指定できるといろいろ便利。下のようにして1から順にサンプル番号をつける
#1から順に1づつ増加させた数を　新しい変数 noに入れる。
#表計算ソフトなどで最初からサンプル番号を振っておけば、この作業は不要

ossdata$no<-c(1:length(ossdata$id))

#サンプル番号20,21,43のデータを見てみる
# | は　　論理記号の　or
ossdata[ossdata$no== 20 | ossdata$no== 21 | ossdata$no== 43,]



・ Cook's distanceプロット
　横軸にサンプルの番号。
　縦軸にCook's distance。

　Cook's distanceは、
　　そのサンプルを除いて回帰分析したときの予測値-全データを用いて推定したときの予測値
　に比例する値。この値が1よりも大きいサンプルは要注意。

図表 Cook's distanceプロット




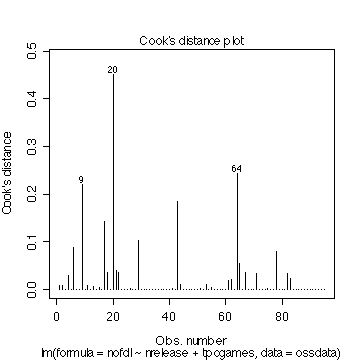
○残差分析で、問題があった場合の、いろいろな対策

・はずれ値
　入力ミスのチェック
　他の説明変数の可能性の追加
　対数化などの変数変換
　そのサンプルを除外する（はずれ値ダミーを入れる）。
#特定のサンプルをはずした分析
# データセット(オブジェクト)の名前の後に
#[-はずしたいオブザベーションの番号,]
#のように指定。

#20番目のオブザベーションをはずしたいときは、次のように。
result2<-lm(nofdl~nrelease+tpcgames,ossdata[-20,])
summary(result2)

#複数を除く場合は、一度に一つしかはずせないので、指定を繰り返した新しいデータセットをつくる。
#　20,21,43番目のオブザベーションをはずしたいとき
#そのオブザベーション毎に異常値ダミーをつくるのも一つの手

ossdata$dum20<-matrix(0,length(ossdata$id),1)
ossdata$dum20[20]<-1

ossdata$dum21<-matrix(0,length(ossdata$id),1)
ossdata$dum21[21]<-1

ossdata$dum43<-matrix(0,length(ossdata$id),1)
ossdata$dum43[43]<-1

res2<-lm(nofdl~nrelease+tpcgames+dum20+dum21+dum43,ossdata)
summary(res2)



・変数の変換
　Q-Qプロットをみると正規分布とのずれがありそう。
　また、予測値-残差プロットをみても予測値が大きくなるほど残差（の絶対値）が大きくなるようにもみえる。
#予測値と残差の相関をみてみる
cor(result2$fitted.values,result2$residuals)

#予測値と残差の[絶対値]の相関をみてみる
cor(result2$fitted.values,abs(result2$residuals))


このような場合によく行われるのが対数変換。
#被説明変数についてのヒストグラムとボックスプロット
hist(ossdata$nofdl)
#あきらかに正規分布ではない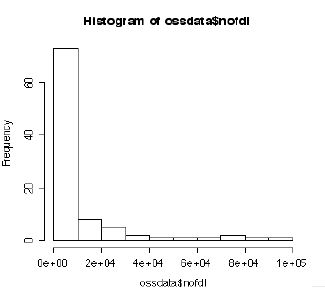


#ボックスプロット（箱ひげ図）
boxplot(ossdata$nofdl)

# 四角い部分は下から第1、２、３四分位点を示す。（第２四分位点は中央値）
#上下に伸びるＴもしくは逆さまのＴは
# 極値=中央値±(第3四分位 - 第1四分位)*1.5
#　極値の範囲外にあるサンプルは　はずれ値　と呼ばれる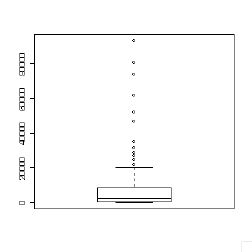

#自然対数をとったものを新しい変数 lnofdl として定義
#log()は自然対数。　　log10()は10を体とする対数

ossdata$lnofdl<-log10(ossdata$nofdl)

hist(ossdata$lnofdl)
#目で見た感じは目盛りの切り方によって若干異なるが、生の変数よりは正規分布に近い。
hist(ossdata$lnofdl,breaks=c(1,2,3,4,5,6))
hist(ossdata$lnofdl,breaks=c(1,1.5,2,2.5,3,3.5,4,4.5,5,5.5,6))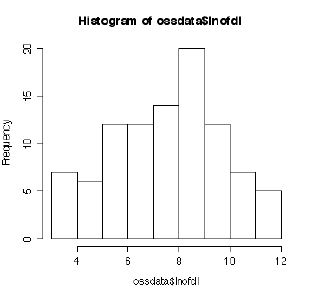


#上ではQ-Qプロットが自動的に出力されたが、qqnorm()コマンドを使えば明示的に出力される。
qqnorm(ossdata$nofdl)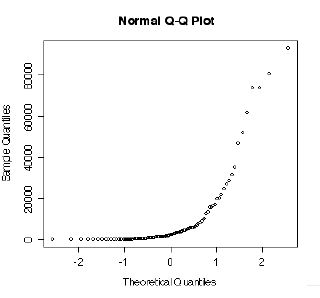

qqnorm(ossdata$lnofdl)
#対数変換した方が直線に近くなっている。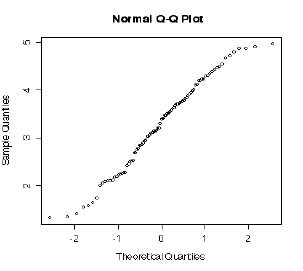


#箱ひげ図をみても、はずれ値（極値の外へのプロット）はなくなった。

boxplot(ossdata$lnofdl)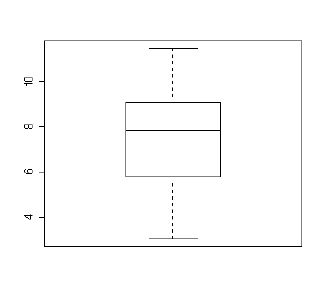
re2<-lm(lnofdl~nrelease+tpcgames,ossdata)
summary(res2)

#Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 2.860385 0.115268 24.815 < 2e-16 ***
#nrelease 0.034430 0.007148 4.817 5.72e-06 ***
#tpcgames 0.400312 0.239651 1.670 0.0982 .
#---
#Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

#Residual standard error: 0.8268 on 92 degrees of freedom
#Multiple R-Squared: 0.2266, Adjusted R-squared: 0.2097
#F-statistic: 13.47 on 2 and 92 DF, p-value: 7.371e-06

plot(res2)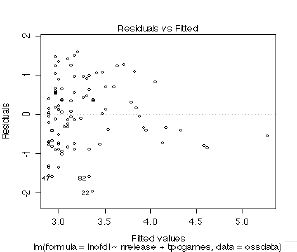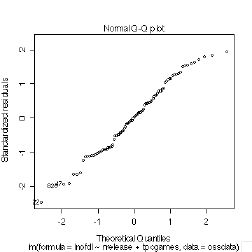





・説明変数についても見てみる
hist(ossdata$nrelease)
boxplot(ossdata$nrelease)

#同様に対数化したものを定義して回帰
ossdata$lnrelease<-log10(ossdata$nrelease)
res3<-lm(lnofdl~lnrelease+tpcgames,ossdata)
summary(res3)
#Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 2.3556 0.1505 15.657 < 2e-16 ***
#lnrelease 1.1364 0.1687 6.735 1.39e-09 ***
#tpcgames 0.2986 0.2205 1.354 0.179
#Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
#Residual standard error: 0.7571 on 92 degrees of freedom
#Multiple R-Squared: 0.3513, Adjusted R-squared: 0.3372
#F-statistic: 24.92 on 2 and 92 DF, p-value: 2.252e-09

plot(res3)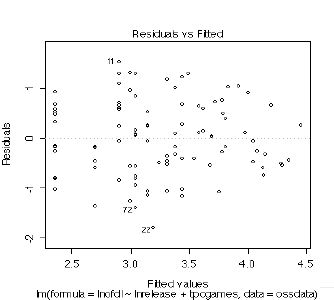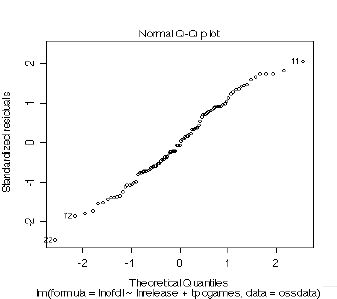

　変数の変換によって、推定結果が次のようになった。


図表　推定結果のまとめ

 

オリジナル変数

従属変数についてlog10変換 従属変数とあわせて説明変数についてもlog10変換
nrelease 481.2*** 0.034430***  
log10(nrelease)     1.1364***
tpcgames 14158.7*** 0.400312* 0.2986
切片 3058.4 2.860385*** 2.3556***
R2 0.175 0.2266 0.3513
修正R2 0.1571 0.2097 0.3372

注）***　1％水準で有意　　　**　5％水準で有意　　*　10％水準で有意


・注意）
　単純に対数化したが、３つめのモデルでは次の式を推定したことになる。

　log10(nofdl)=β1log10(nrelease)+β2tpcgames +β0
つまり
 nofdl=10β1log10(nrelease)+β2tpcgames +β0


　従属変数と説明変数を対数変換するということは、(価格)弾力性=一定という仮説を置いたのと同等になる。

　なぜならば、

log (y) =βlog(x) + β0

 y =eβlog(x) + β0= xβ * eβ0


 dy/dx =β xβ-1eβ0


　弾力性は次式

(dy/y)/(dx/x) =(dy/dx)*(x/y) =(β xβ-1eβ0) x/ (xβ * eβ0 )=β


注）対数の底は10でもeでも結果は同じ。


(2)非線型性への対応
　上記の変数変換で対応可能な場合もある。
　非線型モデルをあてはめた方がよい場合もある。詳しくは省略。
　　例　　y= β1Ｘ　+　β2Ｘ2　+　β3Ｘ3


(3)多重共線性

　回帰分析の前提：説明変数が線型独立。

・この仮定が満たされていないときの症状：不安定な推定結果
　サンプルをいくつか除くと、推定結果が大きく変化。
　変数を除いたり加えたりすると、推定結果が大きく変化。
　直感的に見ておかしな符号
　有意になりそうな変数が有意とならない（標準誤差が大きく、t値が小さい）。

・次の二つに注意する必要がある。
　　(a)説明変数間に高い相関がないか？
　　(b)説明変数と他の説明変数の線敬和との間に高い相関がないか？

　前者については変数間での相関をみればわかる。後者については相関をみるだけではわからないことも多い。

　例１　ダミー変数の定義をしすぎている場合には(b)が生じる。

　　　例　性別ダミーを二つ定義した場合
dmale,
dfemale
　については、下記の関係がある。

dmale+dfemale=1
　　つまり
　　　dmale=1-dfemale

　これら二つの変数を説明変数として使うことは不適切。

　　例２　開発段階ダミーをすべて入れてしまったとき。
　幸いにも、R言語は問題があることを教えてくれる。

ossdata$devst2<-matrix(0,length(ossdata$devstage),1)
ossdata$devst2[ossdata$devstage==2]<-1

ossdata$devst3<-matrix(0,length(ossdata$devstage),1)
ossdata$devst3[ossdata$devstage==3]<-1

ossdata$devst4<-matrix(0,length(ossdata$devstage),1)
ossdata$devst4[ossdata$devstage==4]<-1

ossdata$devst5<-matrix(0,length(ossdata$devstage),1)
ossdata$devst5[ossdata$devstage==5]<-1

ossdata$devst6<-matrix(0,length(ossdata$devstage),1)
ossdata$devst6[ossdata$devstage==6]<-1

res<-lm(nofdl~nrelease+devst2+devst3+devst4+devst5,ossdata)
summary(res)

#Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 25735.9 8870.3 2.901 0.00468 **
#nrelease 465.2 158.1 2.943 0.00414 **
#devst2 -26367.0 10723.3 -2.459 0.01587 *
#devst3 -24740.9 9776.9 -2.531 0.01315 *
#devst4 -23568.0 9382.2 -2.512 0.01381 *
#devst5 -17737.0 9103.1 -1.948 0.05451 .

#定義したすべてを入れて説明
res2<-lm(nofdl~nrelease+devst2+devst3+devst4+devst5+devst6,ossdata)
summary(res2)

#Coefficients: (1 not defined because of singularities)
#　変数の一つは、説明変数間の共分散行列が　特異　であったため用いられなかったというメッセージ
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 25735.9 8870.3 2.901 0.00468 **
#nrelease 465.2 158.1 2.943 0.00414 **
#devst2 -26367.0 10723.3 -2.459 0.01587 *
#devst3 -24740.9 9776.9 -2.531 0.01315 *
#devst4 -23568.0 9382.2 -2.512 0.01381 *
#devst5 -17737.0 9103.1 -1.948 0.05451 .


・多重共線性をチェックするための指標：条件数 condition number
　説明変数の相関係数行列の固有値 eigen valueをλ。
　説明変数が k個の場合、相関係数行列にはk個の固有値が存在する。
　　　
　このうち最大の固有値をλmax
　最小の固有値をλmin
　とすると、条件数κは次式で与えられる。




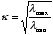
　もとの説明変数の間に完全な直線関係がある場合、相関行列の最小の固有値は0となるという性質がある。よってκの値が大きいほど、多重共線性の恐れがあることを意味する。

　上の式より、κ>1だが経験的に、条件数κが15を越えているときには、多重共線性があるとされる。30を越えるような場合には、対策を考えた方がよい。

　このような場合、下記のような対策が必要。

　説明変数の絞り込み：相関の高い変数群があれば、一つのみを説明変数として使う。
　説明変数の集約：相関の高い変数を加えて新しい変数をつくる、主成分分析、因子分析などによって相関の低い（ない）新しい変数をつくり、それらを用いる。


例　上記のdevstageダミーについて条件数を計算してみる


#相関行列を計算するため新しく別のデータセットに。
a<-data.frame(ossdata$nrelease,ossdata$devst2,ossdata$devst3,ossdata$devst4,ossdata$devst5,ossdata$devst6)

#相関行列作成
cr<-cor(a)
cr
#変数間の相関。非常に高い相関はみられない。
#これだけでは線型独立か否かはわかりにくい。。
# ossdata.nrelease ossdata.devst2 ossdata.devst3 ossdata.devst4
#ossdata.nrelease 1.00000000 -0.17250438 -0.2039430 0.2126873
#ossdata.devst2 -0.17250438 1.00000000 -0.1364683 -0.1812201
#ossdata.devst3 -0.20394303 -0.13646831 1.0000000 -0.2689474
#ossdata.devst4 0.21268731 -0.18122009 -0.2689474 1.0000000
#ossdata.devst5 0.05449983 -0.26994300 -0.4006205 -0.5319952
#ossdata.devst6 0.01745612 -0.06357621 -0.0943530 -0.1252940
# ossdata.devst5 ossdata.devst6
#ossdata.nrelease 0.05449983 0.01745612
#ossdata.devst2 -0.26994300 -0.06357621
#ossdata.devst3 -0.40062049 -0.09435301
#ossdata.devst4 -0.53199518 -0.12529400
#ossdata.devst5 1.00000000 -0.18663625
#ossdata.devst6 -0.18663625 1.00000000

#固有値の計算
#eigen(行列の入っているデータセット名)
#で固有値を計算してくれる
ev<-eigen(cr)
ev

#固有値 6変数なので６個計算される。　　10-16と0に極めて近いものがある。
#$values
#[1] 1.567999e+00 1.490406e+00 1.132193e+00 1.060070e+00 7.493321e-01
#[6] -8.881784e-16

#固有ベクトル　i列めは、上のi番目の固有値に対応する。これに±をつけたもの二つが存在する。
#$vectors
# [,1] [,2] [,3] [,4] [,5] [,6]
#[1,] 0.03312105 0.57092965 -0.11965781 -0.09368358 0.80613133 3.249924e-16
#[2,] 0.11076594 -0.32023099 0.79640835 0.12134588 0.35456416 -3.323796e-01
#[3,] 0.21884350 -0.55453819 -0.58758651 0.07454660 0.30519649 -4.479229e-01
#[4,] 0.57964685 0.48072747 0.01321388 0.19994914 -0.33908493 -5.270463e-01
#[5,] -0.77242101 0.17989474 -0.04083312 0.08725759 -0.09159208 -5.944185e-01
#[6,] 0.07820965 -0.02275568 0.06569541 -0.96090989 -0.08901652 -2.403701e-01

#条件数=sqrt(最大の固有値/最小の固有値）
#固有値がev$valuesに入っているので次のように計算
ra<-sqrt(abs(max(ev$values)/min(ev$values)))
ra

#[1] 42016787
#15よりも大きいので多重共線性がある。何かしらの対策が必要。

#devst2を除いてみる
#相関行列を計算するため新しく別のデータセットに。
b<-data.frame(ossdata$nrelease,ossdata$devst3,ossdata$devst4,ossdata$devst5,ossdata$devst6)

#相関行列作成
cr2<-cor(b)
cr2

ev2<-eigen(cr2)
ev2

#$values
#[1] 1.5640608 1.4443809 1.0617505 0.8103489 0.1194589

ra2<-sqrt(abs(max(ev2$values)/min(ev2$values)))
ra2

#[1] 3.618408
#条件数κは15よりも小さくなった。





res2<-lm(nofdl~nrelease+devst3:nrelease+devst4:nrelease+devst5:nrelease+devst6:nrelease,ossdata)
summary(res2)

#Coefficients:
# Estimate Std. Error t value Pr(>|t|)
#(Intercept) 4664.6 2501.4 1.865 0.0655 .
#nrelease -781.5 1632.0 -0.479 0.6332
#nrelease:devst3 810.8 1704.4 0.476 0.6354
#nrelease:devst4 1122.1 1616.2 0.694 0.4893
#nrelease:devst5 1394.3 1606.1 0.868 0.3877
#nrelease:devst6 3594.8 1711.9 2.100 0.0386 *
#---
#Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

#Residual standard error: 16860 on 89 degrees of freedom
#Multiple R-Squared: 0.2359, Adjusted R-squared: 0.193
#F-statistic: 5.497 on 5 and 89 DF, p-value: 0.0001865

plot(res2)

#devst3とnreleaseとの積
ossdata$dev3nrel<-ossdata$devst3*ossdata$nrelease
ossdata$dev4nrel<-ossdata$devst4*ossdata$nrelease
ossdata$dev5nrel<-ossdata$devst5*ossdata$nrelease
ossdata$dev6nrel<-ossdata$devst6*ossdata$nrelease

#相関行列を計算するため新しく別のデータセットに。
a<-data.frame(ossdata$nrelease,ossdata$dev3nrel,ossdata$dev4nrel,ossdata$dev5nrel,ossdata$dev6nrel)

#相関行列作成
cr<-cor(a)
cr




参考）それぞれの固有ベクトルは直交している。

t()　　　行列（ベクトル）を転置する（行と列を入れ替える）。
例1
ev$vector
# [,1] [,2] [,3] [,4] [,5] [,6]
#[1,] 0.03312105 0.57092965 -0.11965781 -0.09368358 0.80613133 3.249924e-16
#[2,] 0.11076594 -0.32023099 0.79640835 0.12134588 0.35456416 -3.323796e-01
#[3,] 0.21884350 -0.55453819 -0.58758651 0.07454660 0.30519649 -4.479229e-01
#[4,] 0.57964685 0.48072747 0.01321388 0.19994914 -0.33908493 -5.270463e-01
#[5,] -0.77242101 0.17989474 -0.04083312 0.08725759 -0.09159208 -5.944185e-01
#[6,] 0.07820965 -0.02275568 0.06569541 -0.96090989 -0.08901652 -2.403701e-01

t(ev$vector)
# [,1] [,2] [,3] [,4] [,5] [,6]
#[1,] 3.312105e-02 0.1107659 0.2188435 0.57964685 -0.77242101 0.07820965
#[2,] 5.709297e-01 -0.3202310 -0.5545382 0.48072747 0.17989474 -0.02275568
#[3,] -1.196578e-01 0.7964084 -0.5875865 0.01321388 -0.04083312 0.06569541
#[4,] -9.368358e-02 0.1213459 0.0745466 0.19994914 0.08725759 -0.96090989
#[5,] 8.061313e-01 0.3545642 0.3051965 -0.33908493 -0.09159208 -0.08901652
#[6,] 3.249924e-16 -0.3323796 -0.4479229 -0.52704628 -0.59441848 -0.24037009


ベクトル1 %*% ベクトル2　ベクトル1と2の内積を計算する。
例 1番目の固有ベクトルと2番目の固有ベクトルの内積
t(ev$vector[,1]) %*% ev$vector[,2]
# [,1]
#[1,] -1.978100e-18


例 1番目の固有ベクトルと3番目の固有ベクトルの内積
t(ev$vector[,1]) %*% ev$vector[,3]

# [,1]
#[1,] 1.521965e-16

#内積が0ということは、ふたつのベクトルが直交（相関が0）ということ。


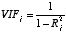
参考)VIF(variance inflation factor)も多重共線性の判定に使われる。

VIFi: 説明変数 xiのVIF は次式で与えられる。


　ただしRi2はxiを被説明変数、これ以外のすべての説明変数を説明変数としたときのR2。
　変数xiが他の説明変数によって完全に説明されているときはRi2=1となる。
　VIF が大きい変数ほど他の変数（の線形結合）との相関が高いことを意味する。



#各説明変数について、他の説明変数で説明する。

r<-lm(nrelease~dev3nrel+dev4nrel+dev5nrel+dev6nrel,ossdata)
summary(r)

r<-lm(dev3nrel~nrelease+dev4nrel+dev5nrel+dev6nrel,ossdata)
summary(r)

r<-lm(dev4nrel~nrelease+dev3nrel+dev5nrel+dev6nrel,ossdata)
summary(r)

r<-lm(dev5nrel~nrelease+dev3nrel+dev4nrel+dev6nrel,ossdata)
summary(r)

r<-lm(dev6nrel~nrelease+dev3nrel+dev4nrel+dev5nrel,ossdata)
summary(r)

#VIF=1/(1-R2)を計算するまでもなく、R2が極めて大きい。


参考）固有値、固有ベクトルについて

　行列 A
　行列Aのi番目の固有値　λi
　上に対応する固有値ベクトル　ei
　とすると、次式の関係がある。

A ei=λiei