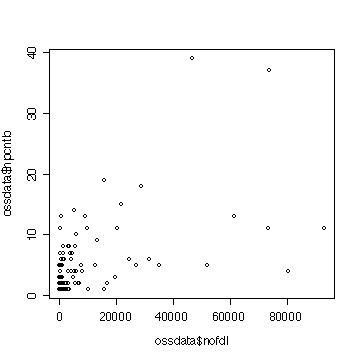
cor(ossdata$nofdl,ossdata$npcntb)
#[1] 0.5172402
3 メトリックな変数を別の変数で説明する(重回帰分析)
|
内容 |
1)分析の目的と手順
例)マーケティングミックス:市場反応(認知率の増加、売上の増加など)を引き起こすことが目的。
市場の反応とマーケティングミックスとを関連づけた分析が必要。
基準変数(従属変数、被説明変数)→市場の反応(認知率、ブランドへの好意度、売上 など)
独立変数(説明変数) →マーケティングミックス(製品の属性、価格、広告コピー、露出量など)
→ 基準変数(被説明変数)を説明変数で説明する。
重回帰分析の手順
|
理論、仮説の決定 ↓ 変数の決定 理論や仮説を検証するために妥当な変数を選択。 ↓ 予備分析 説明変数を被説明変数との関係、説明変数間の関係、はずれ値の有無などをチェック。 ↓ 重回帰分析の実施 プログラムを書き推定を行う。 ↓ モデルの全体的なあてはまりのチェック R2やF検定の結果よりモデルの全体的なあてはまりをチェック。 ↓ モデルの部分的なあてはまりのチェック 個々の説明変数のt検定の結果を解釈 ↓ 変数の追加・削除 説明していない変数を削除したり、説明しそうな変数を加える。 ↓ 回帰診断 残差分析などにより、重回帰分析の仮定が成立しているか、はずれ値はないかなどをチェック。 ↓ (必要ならば)モデルの改訂 変数の組み合わせを変更したり、はずれ値を除外して再度推定。 ↓ 結論 |
plot(ossdata$nofdl,ossdata$npcntb) cor(ossdata$nofdl,ossdata$npcntb) #[1] 0.5172402 |
図 プロットの結果
plot(ossdata$nmsgbug,ossdata$npcntb)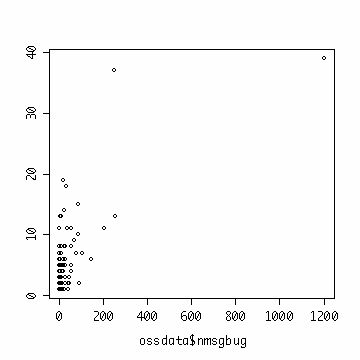 cor(ossdata$nmsgbug,ossdata$npcntb) #[1] 0.5172402 |
それぞれ比例関係があるようにみえる(その他の変数についても同様にできるが、省略)。
→データにあてはまるような直線をみつけるのが、(重)回帰分析。
・単回帰分析
このグラフで、データにもっともよくあてはまるような「直線」をみつける。
つまり、
開発者数 = β1ダウンロード数 + 切片
↓
y = β1x + β0
と定式化して、β1、β0推定することになる。
β1 :偏回帰係数 partial regression coefficient →直線の傾き
β0:切片 intercept→x= 0のときの yの値
| lm( 非説明変数~説明変数,オブジェクト名) 回帰分析(を含む線形モデルの推定を)行う。 |
|
例)y=β0+β1x1+β2x2+β3x3+β4x4;の重回帰モデルを推定する場合には下のように。 lm (y1~x1+x2+ x3+ x4) 切片β0は指定しなくてもよい result<-lm(y~x) のように指定するとオブジェクトの中に下記変数が格納される。 fitted 推定された係数とデータを用いて計算した従属変数の値。 y^ =β0^+β1^x1+β2^x2+β3^x3+β4^x4 residual 残差=y-y^ coefficient 推定された回帰係数 |
|
#回帰分析の結果を オブジェクト result に入れる result<-lm(ossdata$npcntb~ossdata$nofdl) #参考 , のあとにオブジェクト名を指定すれば、モデルの指定式の中ではオブジェクト名は不要。 result<-lm(npcntb~nofdl,ossdata) #結果を表示させる summary(result) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 3.870e+00 6.231e-01 6.211 1.46e-08 *** # 切片の 推定値 標準誤差 t値 p値 と有意水準 #ossdata$nofdl 1.716e-04 2.944e-05 5.828 8.01e-08 *** # この変数の 推定値 標準誤差 t値 p値 と有意水準 #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 # #Residual standard error: 5.358 on 93 degrees of freedom #残差の自由度=サンプル数-推定したパラメーターの数 # =95-2 #Multiple R-Squared: 0.2675, Adjusted R-squared: 0.2597 # R2と修正R2 #F-statistic: 33.97 on 1 and 93 DF, p-value: 8.01e-08 # モデル全体についてのF検定の結果(帰無仮説すべてのβ=0) #----------------- #このように計算された結果オブジェクトには推定(結果)についての情報が格納されている。names関数で、オブジェクトに含まれている変数の名前を見ることができる。 names(result) #いつもと同じように オブジェクト名$変数名とすれば、それぞれの変数を利用できる。 #推定結果をあてはめた予測値:推定した回帰係数と説明変数を用いて計算した被説明変数の値 result$fitted.values #残差=実際の値-fitted.values result$residuals #見やすいように必要な部分を別のデータセットに入れる # 被説明変数 ,説明変数 予測値 残差 ys<-data.frame(ossdata$npcntb,ossdata$nofdl,result$fitted.values,result$residuals) ys #residual =実際の値-fitted.valuesとなっていることがわかる。 # ossdata.npcntb ossdata.nofdl result.fitted.values result.residuals #1 6 31496 9.273904 -3.27390415 #2 13 8907 5.398010 7.60198988 #3 3 126 3.891338 -0.89133761 #4 1 2524 4.302794 -3.30279424 #5 2 122 3.890651 -1.89065127 |
|
#分散分析表も出力してみる。 aov(result) #Call: # aov(formula = result) #Terms: # nofdl と 残差Residual # nofdl Residuals #Sum of Squares 975.2163 2669.9416 #変数によって説明される部分と、残差の二乗和 #Deg. of Freedom 1 93 #自由度 #Residual standard error: 5.358083 #Estimated effects may be unbalanced #実際の被説明変数と、説明変数をプロットしてみる plot(ossdata$nofdl,ossdata$npcntb) #推定された偏回帰係数を用いて直線を描く #abline(切片,傾き) #のように指定すると y=切片+傾き*xという直線を現在の散布図に加える。 result$coefficient #ここに推定された係数が格納されている。 #(Intercept) nofdl #3.8697181174 0.0001715832 #それぞれ次のようにして指定。 abline(result$coefficient[1],result$coefficient[2]) 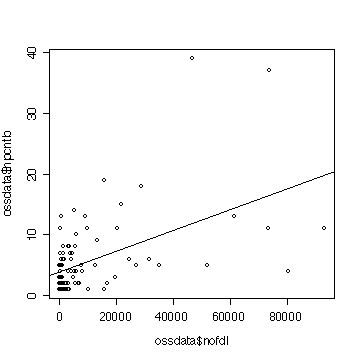
|
|
#実際の被説明変数と予測値をプロットしてみる plot(ossdata$npcntb,result$fitted.values) 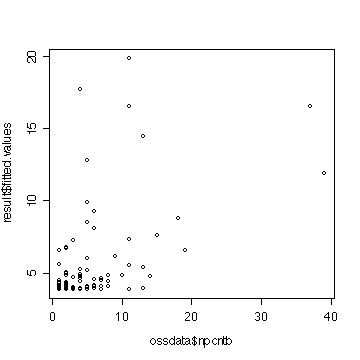 |
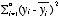 :データの(平均からの)分散
:データの(平均からの)分散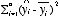 :回帰モデルによって説明されるデータの分散
:回帰モデルによって説明されるデータの分散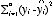 :回帰モデルと実績値との乖離→回帰モデルによって説明されないデータの分散
:回帰モデルと実績値との乖離→回帰モデルによって説明されないデータの分散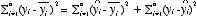
R2:データの分散のうち、回帰モデルによって説明されている分散の割合
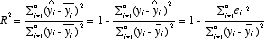
R2は 0〜1の間の値をとる(1に近いほどモデルがよくあてはまっている)。
・自由度修正済み決定係数 adjusted coefficient of determination
→変数を増やすと、それが有意に被説明変数を有意に説明していなくても、一貫してR2は向上。
決定係数は説明変数の数を増やすと見かけ上向上してしまう。
統計学では、parsimonyの原理(節約の原理=おなじ程度の当てはまりならば、より少ない変数、簡単なモデルの方がよい)を採用しているので、使った変数の数(自由度 degree of freedom)を考慮して決定係数を修正したもの。
n:サンプル数 k:パラメーターの数とすると次式で与えられる(パラメーターの数=1のときには決定係数と自由度修正済み決定係数は一致する。)。
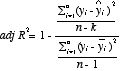
・F検定
複数の説明変数がある時に意味がある(一つのときには偏回帰係数のt検定で充分)。
帰無仮説β1=β2=...βk-1=0 (どの説明変数も従属変数を説明していない。) を検定
k:推定されたパラメーターの数(定数項を含む)
n:サンプル数
n-k:残差の自由度
モデルによって説明される分散: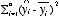
モデルによって説明されない分散(残差の分散):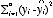
とすると、次式のFは自由度 k-1、n-kのF分布に従う。
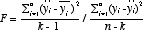
この値をF(kー1,nーk)と比較。αを有意水準として、
F≧Fα(kー1,nーk)のときには、帰無仮説β1=β2=...βk-1=0を棄却する。
→少なくともどれかは0ではない。少なくとも1つの変数が従属変数を有意に説明している。
・t検定:推定されたパラメーター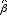 =βdという帰無仮説を検定。
=βdという帰無仮説を検定。
帰無仮説: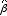 =βd
=βd
次の統計量 tは、自由度 n-k-1のt分布に従う(n:サンプル数。 k:パラメータの数)。
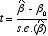
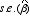 :パラメータβの標準誤差。
:パラメータβの標準誤差。
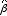 :パラメータβの推定値。
:パラメータβの推定値。
|t|>tα/2(n-k-1)のとき仮説は棄却される。
|t|<tα/2(n-k-1)のとき仮説は棄却されない。
→回帰分析においてもっとも重要なのは、説明変数が従属変数を有意に説明しているか否か(推定された偏回帰係数が0か否か→β0=0):次式で t値を算出2 。
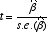
|
#2変数の場合は右辺に + で二つの変数を追加すればよい result2<-lm(npcntb~nofdl+nmsgbug,ossdata) summary(result2) #----------------- #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 3.640e+00 4.986e-01 7.300 9.99e-11 *** #ossdata$nofdl 8.954e-05 2.604e-05 3.439 0.00088 *** #ossdata$nmsgbug 2.774e-02 3.782e-03 7.333 8.55e-11 *** #--- #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 4.28 on 92 degrees of freedom #Multiple R-Squared: 0.5377, Adjusted R-squared: 0.5277 #F-statistic: 53.51 on 2 and 92 DF, p-value: 3.841e-16 aov(result2) #Call: # aov(formula = result2) #Terms: # nofdl nmsgbug Residuals #Sum of Squares 975.2163 984.9564 1684.9851 #Deg. of Freedom 1 1 92 #Residual standard error: 4.279609 #Estimated effects may be unbalanced #1変数の場合と同様にプロットしてみる。ただし説明変数が二つあるので2枚のグラフ。 #実際の被説明変数と、説明変数をプロットしてみる plot(ossdata$nofdl,ossdata$npcntb) #推定された偏回帰係数を用いて直線を描く result2$coefficient abline(result2$coefficient[1],result2$coefficient[2]) #もう一つの説明変数についても同様 plot(ossdata$nmsgbug,ossdata$npcntb) abline(result2$coefficient[1],result2$coefficient[3]) #実際の被説明変数と予測値をプロットしてみる plot(ossdata$npcntb,result2$fitted.values) |
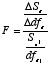
|
#上の例では #変数が一つの場合 # nofdl Residuals #Sum of Squares 975.2163 2669.9416 #Deg. of Freedom 1 93 #残差平方和は 2669.9416 #残差の自由度は 93 #変数を追加した場合 #Terms: # nofdl nmsgbug Residuals #Sum of Squares 975.2163 984.9564 1684.9851 #Deg. of Freedom 1 1 92 #残差平方和は 1684.9851 #残差の自由度は 92 #Fを計算 delta.Se<- 2669.9416-1684.9851 delta.dfe<- 93-92 F<-delta.Se/delta.dfe/(2669.9416/93) F #[1] 34.30822 pf(F,delta.dfe,93,lower.tail=FALSE) #pf(F値,自由度1,自由度2):F分布のパーセント点を求める関数。 #7.051216e-08 #p値 #ここでの帰無仮説 #2つのモデルで残差は減少していない が棄却される。 |
|
#もう一つ変数を入れてみる result3<-lm(npcntb~nofdl+nmsgbug+nrelease,ossdata) summary(result3) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 4.0290647 0.5902670 6.826 9.51e-10 *** #nofdl 0.0001013 0.0000277 3.658 0.000425 *** #nmsgbug 0.0270758 0.0038111 7.105 2.62e-10 *** #nrelease -0.0480682 0.0393045 -1.223 0.224500 #--- #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 4.268 on 91 degrees of freedom #Multiple R-Squared: 0.5452, Adjusted R-squared: 0.5302 #F-statistic: 36.37 on 3 and 91 DF, p-value: 1.538e-15 |
|
このようにシングルアンサー変数の場合には、その変数の水準の数-1個のダミー変数を定義して回帰分析の説明変数に用いる。 「水準」 変数がとることができる値が何通りあるか? 変数が 0、1、2の値をとるときは 3水準 0、1の値をとるときは2水準。 |
| 切片 | 傾き | ||
| 1 | ダミー変数を入れない | ダミー変数を入れない |
グループ間でパラメーターに違いがない。 y = β* x + β0 |
| 2 | ダミー変数を入れる | ダミー変数を入れない |
傾きは同じだが、切片が異なる。 y = β1* x + β0 + βd0 *dum |
| 3 | ダミー変数を入れない | ダミー変数を入れる |
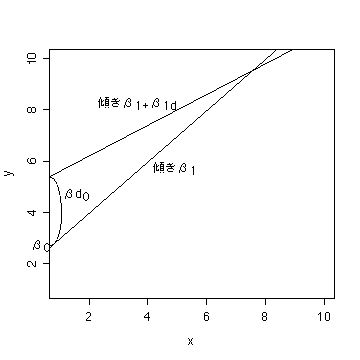
切片は同じだが、傾きが異なる。 y = (β1+β1d *dum)* x + β0 |
| 4 | ダミー変数を入れる | ダミー変数を入れる |
切片、傾きとも異なる。 y = (β1+β1d *dum)* x + β0 + βd0 *dum |
|
result1<-lm(nofdl~nrelease,ossdata) summary(result1) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 4914.1 2397.8 2.049 0.04324 * #nrelease 504.2 154.3 3.267 0.00152 ** #--- #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 17870 on 93 degrees of freedom #Multiple R-Squared: 0.103, Adjusted R-squared: 0.09333 #F-statistic: 10.68 on 1 and 93 DF, p-value: 0.001521 #AICの算出(後述) AIC(result1) #[1] 2133.893 |
|
result0<-lm(nofdl~tpcgames,ossdata) summary(result0) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 7745 2010 3.854 0.000214 *** #tpcgames 15040 5235 2.873 0.005040 ** #--- #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 18090 on 93 degrees of freedom #Multiple R-Squared: 0.08151, Adjusted R-squared: 0.07163 #F-statistic: 8.253 on 1 and 93 DF, p-value: 0.00504 #0という仮説は棄却できるので説明変数として用いても意味がある。 AIC(result0) #[1] 2136.139 |
|
result2<-lm(nofdl~nrelease+tpcgames,ossdata) summary(result2) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 3058.4 2402.9 1.273 0.20631 #nrelease 481.2 149.0 3.229 0.00172 ** #tpcgames 14158.7 4995.9 2.834 0.00565 ** #--- #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 # nofdl = 481.2 nrelease + 14158.7* tpcgames +3058.4 #が推定された直線。つまり、次の二つの直線を表す。 #tpcgames=1のとき # nofdl = 481.2 nrelease + 14158.7 +3058.4 #tpcgames=0のとき # nofdl = 481.2 nrelease +3058.4 #Residual standard error: 17230 on 92 degrees of freedom #Multiple R-Squared: 0.175, Adjusted R-squared: 0.1571 #F-statistic: 9.758 on 2 and 92 DF, p-value: 0.0001435 #生のデータと推定された二つの直線を描く。 plot(ossdata$nrelease,ossdata$nofdl) abline(result2$coef[1],result2$coef[2]) abline(result2$coef[1]+result2$coef[3],result2$coef[2]) AIC(result2) #2127.941 |
|
#二つの変数の積をとった新しい変数 relgame を作成 ossdata$relgame<-ossdata$nrelease*ossdata$tpcgames #nreleaseと作成した変数 relgame によって説明 result3<-lm(nofdl~nrelease+relgame,ossdata) summary(result3) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 4299.0 2338.6 1.838 0.06925 . #nrelease 413.9 153.7 2.693 0.00842 ** #relgame 890.9 342.3 2.603 0.01077 * --- #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 17340 on 92 degrees of freedom #Multiple R-Squared: 0.1645, Adjusted R-squared: 0.1463 #F-statistic: 9.057 on 2 and 92 DF, p-value: 0.0002566 #上のようにわざわざ新変数を生成しなくても、変数1:変数2 のように、二つの変数をコロン(:)で結んだものを説明変数として指定すれば、上と同じ結果が得られる。 result3<-lm(nofdl~nrelease+nrelease:tpcgames,ossdata) summary(result3) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 4299.0 2338.6 1.838 0.06925 . #nrelease 413.9 153.7 2.693 0.00842 ** #nrelease:tpcgames 890.9 342.3 2.603 0.01077 * #--- #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 17340 on 92 degrees of freedom #Multiple R-Squared: 0.1645, Adjusted R-squared: 0.1463 #F-statistic: 9.057 on 2 and 92 DF, p-value: 0.0002566 AIC(result3) #2129.142 |
|
result4<-lm(nofdl~nrelease+tpcgames+nrelease:tpcgames,ossdata) summary(result4) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 3346.9 2449.7 1.366 0.17523 #nrelease 451.5 156.1 2.893 0.00477 ** #tpcgames 10072.6 7967.8 1.264 0.20940 #nrelease:tpcgames 357.8 542.4 0.660 0.51116 #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 17290 on 91 degrees of freedom #Multiple R-Squared: 0.1789, Adjusted R-squared: 0.1519 #F-statistic: 6.61 on 3 and 91 DF, p-value: 0.0004323 # nofdl = 451.5 nrelease +357.8 nrelease*tpcgames + 10072.6* tpcgames +3346.9 #が推定された直線。つまり、次の二つの直線を表す。 #tpcgames=1のとき # nofdl = (451.5 +357.8 )nrelease + 10072.6 +3346.9 #tpcgames=0のとき # nofdl = (451.5 )nrelease +3346.9 #生のデータと推定された二つの直線を描く。 plot(ossdata$nrelease,ossdata$nofdl) abline(result4$coef[1],result4$coef[2]) abline(result4$coef[1]+result4$coef[3],result4$coef[2]+result4$coef[4]) AIC(result4) #2129.488 |
推定のまとめ表
|
モデル1 |
モデル0 | モデル2 | モデル3 | モデル4 | ||
| nrelease |
504.2** (3.267) |
481.2** (3.229) |
413.9** (2.693) |
451.5** (2.893) |
||
| 傾きへのダミーnrelease*tpccntb |
890.9* (2.603) |
357.8 (0.660) |
||||
| 切片へのダミーtpccntb |
15040** (2.873) |
14158.7** (2.834) |
10072.6 (1.264) |
|||
| 切片 |
4914.1* (2.049) |
7745*** (3.854) |
3058.4 (1.273) |
4299.0 (1.838) |
3346.9 (1.366) |
|
| R2 | 0.103 | 0.08151 | 0.175 | 0.1645 | 0.1789 | |
| 修正R2 | 0.09333 | 0.07163 | 0.1571 | 0.1463 | 0.1519 | |
| 残差平方和 | 29713596953 | 30424668920 | 27327764555 | 27675351736 | 27197720513 | |
| 残差自由度 | 93 | 93 | 92 | 92 | 91 | |
| AIC | 2133.893 | 2136.139 | 2127.941 | 2129.142 | 2129.488 |
|
table(ossdata$devstage) # 2 3 4 5 6 # 8 16 25 42 4 #この変数は本来は1,2,3,4,5,6の値(6水準)をとるが、サンプルには、これが1になるものがない。 #よって5水準-1=4つのダミー変数をとる。 #今回は、2を基準とすることにして、次の4つのダミー変数を定義 #devst3 devstage=3のとき1 そうでないとき0 #devst4 devstage=4のとき1 そうでないとき0 #devst5 devstage=5のとき1 そうでないとき0 #devst6 devstage=6のとき1 そうでないとき0 #matrix(値,行の数,列の数) #devstageに対応するダミー変数を定義して0を入れておく。 ossdata$devst3<-matrix(0,length(ossdata$devstage),1) #ossdata$devstage==3のサンプルのみ、ダミー変数を1にする。 ossdata$devst3[ossdata$devstage==3]<-1 ossdata$devst4<-matrix(0,length(ossdata$devstage),1) #ossdata$devstage==4のサンプルのみ、ダミー変数を1にする。 ossdata$devst4[ossdata$devstage==4]<-1 ossdata$devst5<-matrix(0,length(ossdata$devstage),1) #ossdata$devstage==5のサンプルのみ、ダミー変数を1にする。 ossdata$devst5[ossdata$devstage==5]<-1 ossdata$devst6<-matrix(0,length(ossdata$devstage),1) #ossdata$devstage==6のサンプルのみ、ダミー変数を1にする。 ossdata$devst6[ossdata$devstage==6]<-1 #出力して確かめてみる a<-data.frame(ossdata$devstage,ossdata$devst3,ossdata$devst4,ossdata$devst5,ossdata$devst6) a |
|
#定義した変数を切片に入れて回帰。 res<-lm(nofdl~nrelease+devst3+devst4+devst5+devst6,ossdata) summary(res) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) -631.0 6172.0 -0.102 0.91879 #nrelease 465.2 158.1 2.943 0.00414 ** #devst3 1626.1 7536.0 0.216 0.82966 #devst4 2799.0 7276.8 0.385 0.70142 #devst5 8630.0 6814.4 1.266 0.20866 #devst6 26367.0 10723.3 2.459 0.01587 * #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 17400 on 89 degrees of freedom #Multiple R-Squared: 0.1869, Adjusted R-squared: 0.1412 #F-statistic: 4.091 on 5 and 89 DF, p-value: 0.002172 AIC(res) #2132.564 #定義した変数を傾きに入れて回帰。 res2<-lm(nofdl~nrelease+devst3:nrelease+devst4:nrelease+devst5:nrelease+devst6:nrelease,ossdata) summary(res2) #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 4664.6 2501.4 1.865 0.0655 . #nrelease -781.5 1632.0 -0.479 0.6332 #nrelease:devst3 810.8 1704.4 0.476 0.6354 #nrelease:devst4 1122.1 1616.2 0.694 0.4893 #nrelease:devst5 1394.3 1606.1 0.868 0.3877 #nrelease:devst6 3594.8 1711.9 2.100 0.0386 * #--- #Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 #Residual standard error: 16860 on 89 degrees of freedom #Multiple R-Squared: 0.2359, Adjusted R-squared: 0.193 #F-statistic: 5.497 on 5 and 89 DF, p-value: 0.0001865 AIC(res2) #2126.650 #AICはこちらの方が小さいが、nreleaseの符号が(有意ではないが)マイナスなので多重共線性(後述)の恐れあり。 |
1 R=√R2は、重相関係数と呼ばれる。