
1.いろいろなデータ
財務データ
経済統計
消費者に対するアンケートデータ など
1)データの使い方
(1)事実を記述する。
(2)仮説を検定する。
(3)仮説を発見する。
(1)事実を記述するデータ
・アンケートを行って日米の経営の特徴を比較した例。
日本の方が長期志向であるといった仮説は設定されていないが、市場環境、組織構造、組織革
新などの点を比較するという点については、先行研究の理論的枠組みを参照している。

出所)加護野、野中、榊原、奥村(1993),「日米企業の戦略と組織」,(伊丹、加護野、伊藤編『リーディングス 日本の企業システム 第2巻』),p.107-144
・消費者に対する意識調査を定期的に行った結果:時間と共に価値観が変化していることがよみとれる。

出所)渡部久哲(1994),「消費者行動と価値観の変化」,(飽戸弘編著『消費行動の社会心理学』福村書店),p.152-172
(2)仮説を検証するためのデータ
仮説を設定して、それを検証(検定)するためのデータを収集、分析する。
・継続的取引の規定要因についての仮説の検証例

注)ENJO=β0+β1SIGEN+β2HENDO+β3ZAIKO+β4KOUKOKU
ENJO:仕入先へ指導を行っている企業の割合
SIGEN:研修×給与=関係特殊的資源の重要性
HENDO:受容の不確実性
ZAIKO:在庫調整の容易さ=商品回転率/(流動資産/総資産)
KOUKOKU:広告支出/売上=ブランドロイヤリテイ
出所)成生達彦、鳥居昭夫(1996),「流通における継続的取引関係」,(伊藤秀史編『日本の企業システム』東京大学出版会),p.183-214
・雇用統計をヒストグラムに:入社後、時間が経過するにつれて、企業規模によって給与水準が大きく異なる。


出所)石川経夫(1993),「日本の労働市場の構造 賃金二重構造の理論的検討」,(伊丹、加護野、伊藤編『リーディングス 日本の企業システム 第3巻 人的資源』),p.248-275
・ブランドの二重苦
二つのカテゴリについて、各ブランドのシェア、1回以上購入した人の割合、購入者一人あたりの購入回数を算出し、シェアの順に並べたもの。シェアが上位のブランドほど、浸透率も購入回数も大きくなる傾向がみられる。つまり、下位ブランドは、シェアが低いだけではなくて、浸透率、購入回数も少ないという二重苦を背負っている1
。
他の商品カテゴリ、他の国でもそうなのか?なぜ、そうなるのか?を考えるきっかけとなる。
図表 ブランドの二重苦の例(1988年の1年間のデータを集計)
a)ケチャップ
| ブランド | シェア(%) | 購入した人の割合(浸透率:%) | 購入者一人あたりの購入回数 |
| ブランド1 |
|
|
|
| ブランド2 |
|
|
|
| ブランド3 |
|
|
|
| ブランド4 |
|
|
|
| ブランド5 |
|
|
|
b)ヨーグルト
| ブランド | シェア(%) | 購入した人の割合(浸透率:%) | 購入者一人あたりの購入回数 |
| ブランド1 |
|
|
|
| ブランド2 |
|
|
|
| ブランド3 |
|
|
|
| ブランド4 |
|
|
|
| ブランド5 |
|
|
|
注)ヨーグルトについてはブランドは35あるが、上位5位までの結果のみ示す。
出所)富永純一(1993)「日本におけるブランドの二重苦について」東京大学大学院経済学研究科mimeo.
2.データとの対話のプロセス
→この講義「(数字)データ」との対話
数字データ
・もともと数字で表現されている。
人口、体重、経済成長率 .....
・数字で表現されていないデータを数字で表現する。→ダミー変数化することなどによって可能となる場合もある。
職業、学歴....
これらの数字データをどう扱うか?
1)データとの対話の「プロセス」
図表 データとの対話の「プロセス」
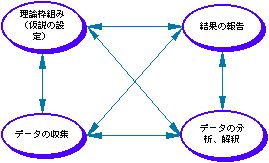
○理論的枠組み・仮説の重要性
例1 アインシュタインの相対性理論と恒星の視差角度の観測
相対性理論によると、重力によって空間がゆがむと予測される。それを確認するために、太陽の重力による恒星からの光のずれを測定した。そのずれの角度は、極めて微小であり、測定しようと思わなければ測定できないものであった。
例2「眼は、それが探し求めているもの以外は見ることができない。探し求めているものは、もともと心の中にあったものである(フランスの警察の科学的犯罪捜査法学校のスローガン)」[村上陽一郎(1974:1986),『近代科学を超えて』,日本経済新聞社(講談社学術文庫に収録、1986年,p.32)]
→インプリケーション
見ようと思ったものしか見えない
→理論的枠組み・仮説(自分たちが何を見たいのか・知りたいのかを明確にすることが必要)は重要
・仮説をもつことのメリット:無駄、的外れな分析をする必要がなくなる。
この授業では、前節の(1)(2)のデータの使い方を学ぶ。
・そうすることのデメリット: 仮説についてのデータしかみえなくなる?
新しい発見がされにくくなる?
理論的な枠組み(仮説として規定される場合もある)
自分たちが何を見たいのか・知りたいのかを明確にするためには?
分析対象とする現象、それを扱う学問分野の知識を身につけておくことが必要。
→各自で身につけることが必要(この講義のメインテーマではない)。
↓ ↑
データの収集、解釈、分析手法・モデル:この講義でのテーマ
図表 データとの対話の具体的プロセスの一例(アンケート調査の場合)
|
|
|
|
|
| 理論的枠組みの決定 | 研究課題や目的を定義し、用いる分析手法を決定する。 | 何が知りたいのか、それを知るためにはどのようなこと(概念)がわかればよいのかを概念レベルで明確にしておく。 | ここがちゃんと決定していないと、まともな分析はできない。なんのための調査、分析かを明確にしておく。 |
| 分析計画の立案 | どのような変数を、どのような方法で測定するか。どのような多変量分析をすればよいか。どのようなサンプルから、どれぐらいのサンプル数を回収するかを決定する。データのコーディング、分析スケジュールなども決定しておく。 | 分析する手法によって、データの形式、必要なサンプル数は異なってくる。 | |
| データの収集 | 質問紙の作成 | データ収集に用いる質問票を作成する。 | アンケート調査の場合、測定したい概念がきちんと測定されているか?回答しやすいかなどを確認しておく。 |
| サンプリング | コストや時間などの制約を考えながら、目的に適したサンプルから、精度高くデータを収集できるようなサンプリング方法、サンプルサイズを決定。 | 見当はずれな相手に質問をしないように。 | |
| 実査 | 調査を実施し、データを収集する。 | 実行段階でのエラーも大きい。問い合わせにはちゃんと応じることが必要。
回収率を高めるために督促することもある。 |
|
| 無効サンプルのチェック | 無回答が多かったり、回答がいい加減で、信頼性が低いサンプルは除外する。 | 無回答が多いからといって、回答者を責めてはいけない。質問紙の構成などに問題はないか?この時点で後悔しても仕方ないので、計画段階で注意しておく。 | |
| データの分析、解釈 | コーディング、データの入力 | データのコーディングを行い、入力するためのフォーム(書式)を決定、作成する。
収集されたデータを入力する。 |
コンピュータで分析するためには、集められたデータを分析に適した形にコード化しなくてはならない。
せっかく集めたデータも、入力ミスがあっては台無し。 |
| データ読み込み | データに変数名をつけて、パッケージで読み込む。 | 分析のときにわかりやすい変数名をつけておくことが重要。 | |
| データの予備分析 | 多変量解析手法では、いろいろな仮定をに基づいてモデルを規定しているものがある。そのような仮定が満たされているかを確認しておく。
複雑な分析を行う前に、記述統計や、グラフ化などをすることによって、はずれ値や非線形な関係がないかなどをチェックする。 |
分析の前提が成立していなければ、どんな多変量解析を行っても無駄。 | |
| モデルの推定、全体的なフィットの評価 | 多変量解析を行う。(仮説設定→検定型ならば、すべての変数をモデルに投入して終わりでもokかもしれないが多重共線性などのチェックは必要。必要ならば)変数の入れ替えなどを行い、分析を繰り返す。複数の分析結果を比較して、最もよいモデルをみつける。 | 一つの分析だけで満足しない。いろんなことを、しかし「系統的に」試してみる。 | |
| 個々の変数の影響を解釈する。 | 最もよいモデルについて、個々の変数がどのように影響を与えているかを解釈する。また、仮説を検証・検定する段階。 | 知りたいことがわかるはずの分析をする。いろいろやれば何か面白いことがわかるという態度はだめ。 | |
| モデルの有効性を検証する。 | 推定されたパラメータと説明変数を用いて、従属変数を推定する。推定された結果と測定されたデータとを比較する。誤差が小さければ有効である。
また、推定されたパラメーター、別のデータセットを用いて推定するという方法もある。 |
データからパラメータを推定しただけでは不十分。
推定されたパラメータを用いてデータが再現されるか、他のデータセットでも同じような結果が得られるかを確認しておくと安心できる。 |
|
| 結果の報告 | 結果を提示する。 | 分析された結果をわかりやすく提示する。 | 「多変量解析」というとビビル相手もいる。ビビらせるために多変量解析を使うこともあるが、分析の結果、何がわかったか?それをわかりやすく伝えることが基本的な考え方。 |
1. データとの対話のツールとしてのR
Rとは、統計解析を行う言語、パッケージ。
特徴
S言語と互換性あり。
簡単なプログラムミングと結果の読み方をマスターすれば、難しい公式を覚えることなく簡単に統計分析を行うことができる。
オープンソースソフトウエア
無料で入手可能
以下の統計パッケージがある(この他にもGauss、Rats、Excelのアドインや別売りの多変量パッケージなどがある)。
図表 主な統計パッケージ
|
|
|
|
|
|
|
| SAS | 必要な統計手法はほぼ、網羅されている。
作成したデータの再利用などが比較的簡単にできる。 ユーザーグループが組織されており、ユーザによって開発されたプログラムも入手可能。コンジョイント分析はマクロで定義される。 個人ではなく、企業、大学などの組織との契約で、買い取りではなく、1年契約で更新するというのが面倒。 |
|
|
|
|
| JMP | SAS/INSIGHTの簡易版。pop-upメニューで表計算ソフト感覚で分析できる。グラフがきれいだが、因子分析など初歩的な多変量解析手法も使えないので、データの予備分析用。 コレスポンデンス分析はできる。
学生ならば下記の本を購入するとおまけで機能限定版のJMP INがついてくる(Win版もある)。 SAS Institute Inc.(1996),JMP IN: ver 3 for Machintosh: Statistical Discovery Software: A Student Edition of JMP,Duxbury Inc. |
|
|
||
| SPSS | 必要な統計手法はほぼ、網羅されている。
WIN版はpop-upメニューから分析できる。 学生にはPC版の特別割引システムが○、一揃え30万円以上のものが6万円程度になる。 |
|
|
|
|
| BMDP | 統計パッケージプログラムの走り。いろいろと細かいルーチンが使えるらしいが、私は使ったことがない。 |
|
|
||
| S | オブジェクト指向の言語で簡単に記述できる。グラフィクスなどがきれいに描けるそう。最近、一部でブームになりつつある。 |
|
WIN | ||
| TSP | 計量経済学で使われる統計モデルが中心なので、因子分析、クラスター分析などは含まれていない。
ロジット分析、プロビット分析が簡単にできる。 最尤推定専用のコマンドが○、最尤関数を与えるだけで(自分で微分しなくても)推定してくれるという優れた機能がある。 パソコン版でもコマンドライン入力もしくは、バッチで処理。パソコン版のstudent TSPというのはpop-upからも使える。 |
|
|
|
|
| SYSTAT | 重回帰分析、因子分析、MDS、クラスター分析などが使え、最適化のルーチンもあるので、これで一通りの分析ができる。
スプレッドシート型のデータエディタと統計、グラフが一体化されているので便利。 ポップアップメニューからでもコマンド入力もできる。 グラフもいろいろあるが、見栄えはあまりよくない。 対話型でも、バッチでも使えるので、同じ処理をたくさんする場合には助かる。 しかし、因子分析では因子得点を算出してくれないので困る。 |
|
|||
| STATISTICA | スプレッドシート型のデータエディタと統計、グラフが一体化されている。重回帰分析、クラスター分析、因子分析などができる。
ただし、完全に対話型で、一ステップづつ分析を進めていくので、慣れた人には冗長。 また、IDによるデータマージもできないのが困る。 |
|
|
||
| Lisp-stat | x-lispベースで統計手法、グラフなどのプログラムがコマンドとして定義されたパッケージ群。
多変量解析のパッケージは見あたらないが、探索的データ解析でのグラフ化の手法に特徴がある。マトリクス演算などがプログラムできるので、自分でプログラムしたい人向け。はやりのopen sourceのフリーウエア。 |
|
|
|
|
| ASP | 下の本に、おまけでついてくるパッケージ。おまけの割には、いろんな分析ができるが、多変量解析としては、重回帰分析と、因子分析しかできない。
DOS版なので、グラフもキャラクタ表示しかできない。 McClave, James T. and P. George Benson(1994),Statistics for Business and Economics 6th ed.,Prentice-Hall |
|
2.使える手法の例(括弧内は各分析を行うSの関数名。
・データフレーム名$変数名 のように指定する。
・ヘルプは
help(コマンド名)
・データの印刷、グラフの作成など 使える変数の尺度、モデルの形
データセットの(印刷)出力 (データセット名のみを指定すれば出力される)
ヒストグラムの作成 hist() メトリック
散布図グラフの作成 plot() メトリック×メトリック
箱ひげ図 poxplot()
幹葉図 stem()
・統計分析
平均 mean()
分散 var()
標準偏差 sqrt(var()) sqrt()は平方根。分散の平方根が標準偏差
中央値 median()
最小値 min()
最大値 max(x)
平均値、4分位点(メディアン)の算出 summarize()
頻度分布表、クロス集計表の作成、検定 table() ノンメトリック×ノンメトリック
χ2検定 chisq.test()
変数間の相関係数の算出 cor() メトリック×メトリック
2つの母集団の平均の差の検定 t検定 t.test(変数~分類変数)
メトリック=ノンメトリック
3つ以上の母集団の差の検定: 分散分析 aov(), anova() メトリック=ノンメトリック
(重)回帰分析 lm() メトリック=メトリック、ノンメトリック
library(mva)として多変量解析のライブラリをロードしておく。
因子分析 factanal() メトリック=因子(メトリック)
主成分分析 princomp 主成分=Σメトリック
階層型クラスター分析 hclust() メトリック
非階層型クラスター分析 kmeans メトリック
・メトリックとノンメトリックな変数:変数の尺度
測定の尺度は次の4つに分類できる。
→尺度によって可能な演算が異なる。→使える手法も限定される。
なお、これらは次の二つに大別される。
ノンメトリック(質的):名目尺度、順序尺度
メトリック(量的):間隔尺度、比率尺度
図表 4つの測定尺度
|
|
|
|
|
| 質的データ
qualitative data もしくはノンメトリックデータ non-metric data |
名目尺度 nominal scale | 対象の分類を示すだけで、順序、間隔などの意味は持たない。
例)性別、職業 例2)下のブランドのうちあなたが買ったことがあるものを選んで下さい。 1.ポッカ 2.ジョージア...... |
頻度のカウント
最頻値 mode |
| 序数尺度 ordinal scale | 対象の順序を示すが、間隔の意味はもたない。
例)次の缶コーヒーのブランドをどれくらい好きでしょうか?それぞれについて、好きな順位を記入して下さい。 |
上に加えて、
中央値 median 最頻値 mode |
|
| 量的データ
quantative data もしくはメトリックデータ metric data |
間隔尺度 interval scale | 数値の違いに間隔の意味があり、差を測ることができる(2と1の差と3と2の差は同じ)。ただし、原点が固定されていない。
例1)摂氏での温度 例2)下に7種類の「缶コーヒー」のブランドが挙げてあります。それぞれのブランドに対して、あなたの好き嫌いの程度をお答えください(1非常に好き。2:好き。3:どちらともいえない。4:嫌い。5:非常に嫌い)。 ・ポッカ 1 2 3 4 5 ・ジョージア 1 2 3 4 5 厳密には等間隔である保証はないが、マーケティングなどでは間隔尺度として扱われることが多い。 |
上に加えて、
平均 mean
|
| 比率尺度 retio scale | 数値の違いに間隔の意味があり、差を測ることができ、原点が固定されているので、比を計算することができる。
例1)体重、人口、所得
|
上に加えて、
調和平均
|
|
分析の目的、変数の尺度に応じて適切な手法を選択する必要がある。
1 Ehrenberg,Goodhardt and Barwise(1990)"Double Jeopardy Revisited,"Journal of Marketing,Vol.54,pp.82-91(これの抄訳は濱岡訳(1994)「(論文翻訳)ブランドの二重苦:再考」『マーケティング・ジャール』1994年、,Vol.13,No.4,pp.19-29)